Contents

Regularization

There are various ways to avoid overfitting of neural networks.

On Loss

Weight Decay

In neural networks, \(L_2\) regularization is often called weight decay. It is easy to incorporate weight decay into the gradient calculation of the loss

\[ \nabla_{\boldsymbol{w}} \lambda\|\boldsymbol{w}\|^{2}=2 \lambda \boldsymbol{w} \]

It brings one more hyperparameter \(\lambda\) to tune. Depending on the data set/task, it can be more/less useful.

Dropout

A part of overfitting in neural networks is that different nodes may capture the same pattern, called unit co-adaptation. We then prevent it by disrupting co-firing patterns.

Dropout [Srivastava et al]

During each training iteration, randomly “remove” some nodes, then run forward and backward propagation to update the gradient of the remaining nodes. In prediction, use all nodes.

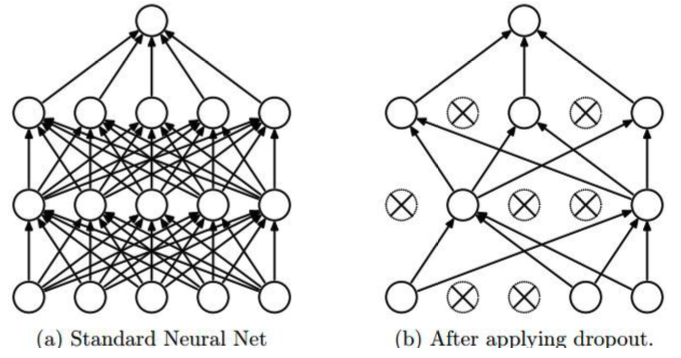
Fig. 164 Dropout [Goodfellow et al.]

With each particular dropout set, we have a different network. An interpretation is, we are training an ensemble of networks with shared parameters, which is a good way to avoid overfitting.

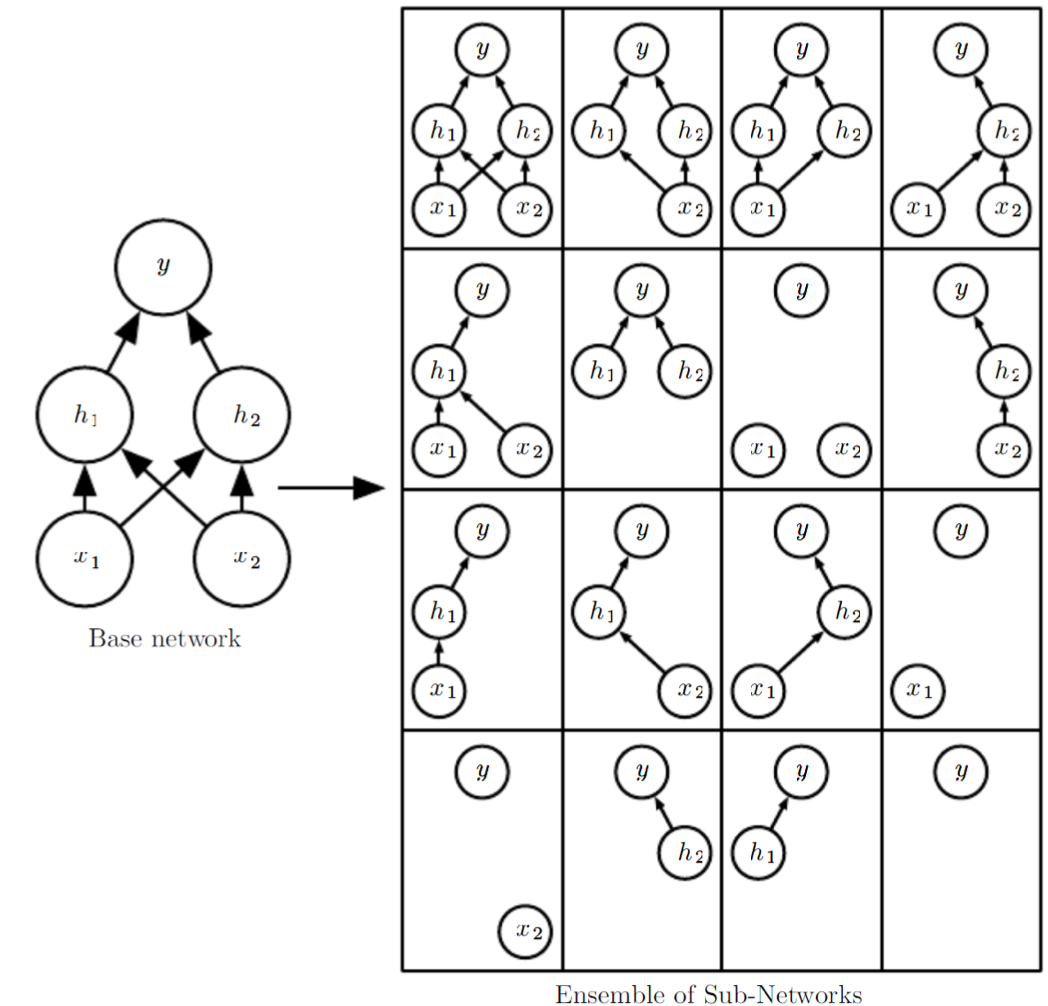
Fig. 165 Dropout as ensemble [Goodfellow et al.]