\(k\)-means clustering¶
Originated by MacQueen (1967), \(k\)-means clustering is an iterative algorithm for clustering. It initialize \(k\) cluster centers, assign each example to its closest center, and re-compute the center, until there is no changes in assignment.
Objective¶
For a given \(k\), the objective is to form clusters \(C_1, \ldots, C_k\) that minimize the within cluster sum of squares (aka total distortion)
where \(\boldsymbol{\mu}\) is the mean or centroid of objects in cluster \(C_i\).
\(k\)-means is NP hard.
Algorithm¶
A standard algorithm for \(k\)-means is Lloyd-Forgy algorithm, which is an heuristic method. For other algorithms, see here.
Lloyd-Forgy algorithm for \(k\)-means clustering
Initialize \(k\) cluster centers \(\boldsymbol{\mu} _1, \ldots, \boldsymbol{\mu} _k\) at random locations.
While True
Assignment step: assign each example \(\boldsymbol{x} _i\) to the closest mean
\[ y_{i}=\operatorname{argmin}_{c}\left\|\boldsymbol{x}_{i}- \boldsymbol{\mu} _{c}\right\| \]Update step: re-estimate each mean based on examples assigned to it
\[ \mu_{c}=\frac{1}{n_{c}} \sum_{y_{i}=c} \boldsymbol{x}_{i} \]where \(n_{c}= \left\vert \left\{\boldsymbol{x}_{i}: y_{i}=c\right\} \right\vert\)
repeat until there are no changes in assignment
With each iteration step of the K-means algorithm, the within-cluster variations (or centered sums of squares) decrease and the algorithm converges.
The standard algorithm often converges to a local minimum, rather than global minimum. The results are affected by initialization.
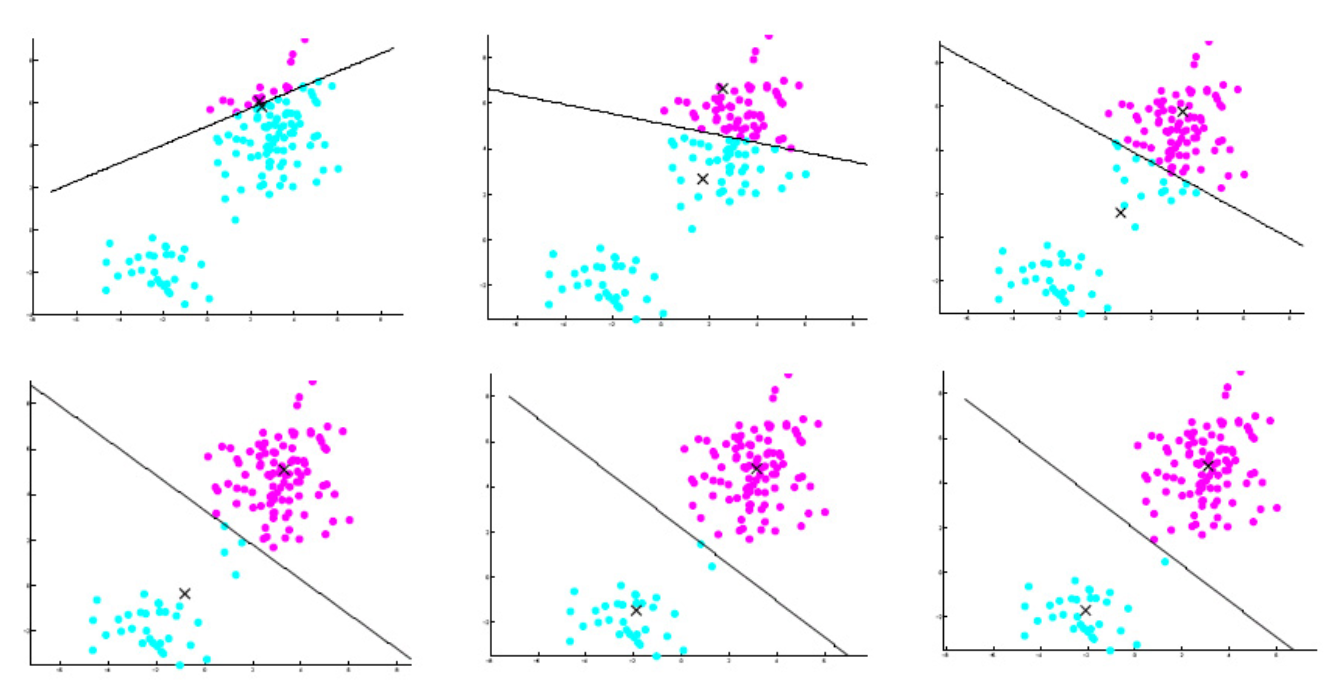
Fig. 115 Iterations in \(k\)-means example [Livescu 2021]¶
Tuning¶
To choose the optimal \(k\), we can plot some measure versus \(k\), e.g. total within-cluster sum of squares, and look for an elbow.
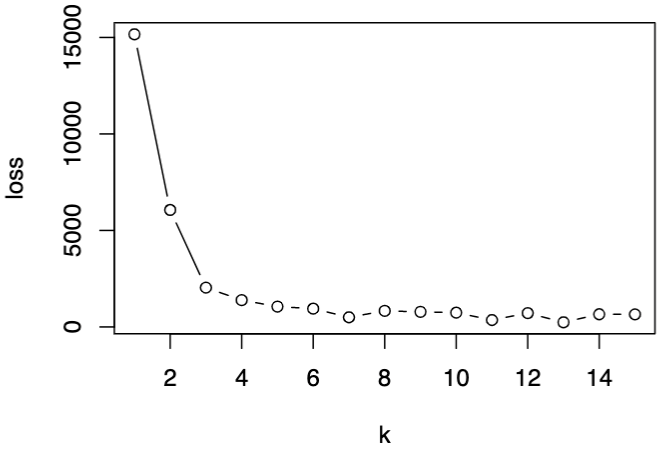
Fig. 116 Within-cluster SS decreases as \(k\) increases.¶
Pros Cons¶
Pros
Work well for clusters with spherical shape and similar size
Cons
Affected by random initialization.
heuristic remedy: try several initializations, keep the result with lowest total distortion \(D\)
Work bad for clusters with non-ideal attributes

Fig. 117 \(k\)-means fail for clusters with non-ideal shapes [Livescue 2021]¶
Relation to¶
Geometrically, \(k\)-means method is closely related to the Voronoi tessellation partition of the data space with respect to cluster centers
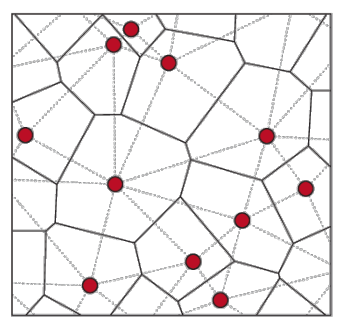
Fig. 118 Illustration of Voronoi tessellation [DJ Srolovitz]¶
Various modifications of \(k\)-means such as spherical \(k\)-means and \(k\)-medoids have been proposed to allow using other distance measures.
Code¶
import numpy as np
def euclidean_distance(x1, x2):
distance = 0
for i in range(len(x1)):
distance += pow((x1[i] - x2[i]), 2)
return np.sqrt(distance)
def centroids_init(k, X):
n_samples, n_features = X.shape
centroids = np.zeros((k, n_features))
for i in range(k):
centroid = X[np.random.choice(range(n_samples))]
centroids[i] = centroid
return centroids
def closest_centroid(sample, centroids):
closest_i = 0
closest_dist = float('inf')
for i, centroid in enumerate(centroids):
distance = euclidean_distance(sample, centroid)
if distance < closest_dist:
closest_i = i
closest_dist = distance
return closest_i
def create_clusters(centroids, k, X):
n_samples = np.shape(X)[0]
clusters = [[] for _ in range(k)]
for sample_i, sample in enumerate(X):
centroid_i = closest_centroid(sample, centroids)
clusters[centroid_i].append(sample_i)
return clusters
def calculate_centroids(clusters, k, X):
n_features = np.shape(X)[1]
centroids = np.zeros((k, n_features))
for i, cluster in enumerate(clusters):
centroid = np.mean(X[cluster], axis=0)
centroids[i] = centroid
return centroids
def get_cluster_labels(clusters, X):
y_pred = np.zeros(np.shape(X)[0])
for cluster_i, cluster in enumerate(clusters):
for sample_i in cluster:
y_pred[sample_i] = cluster_i
return y_pred