Contents

Linear Algebra

reference:

  • Numerical Linear Algebra, Volker Mehrmann link

Matrix Operations

Transpose

Definition

\(\boldsymbol{A} ^\top =\left( a_{ji} \right)\)

Properties

\(\ \)

\[\begin{split} \begin{aligned} \left(\boldsymbol{A}^{\top}\right)^{\top} &=\boldsymbol{A} \\ (\boldsymbol{A}+\boldsymbol{B})^{\top} &=\boldsymbol{A}^{\top}+\boldsymbol{B}^{\top} \\ (\boldsymbol{A} \boldsymbol{B})^{\top} &=\boldsymbol{B}^{\top} \boldsymbol{A}^{\top} \\ \left(\begin{array}{ll} \boldsymbol{A} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{D} \end{array}\right)^{\top} &=\left(\begin{array}{l} \boldsymbol{A}^{\top} & \boldsymbol{C}^{\top} \\ \boldsymbol{B}^{\top} & \boldsymbol{D}^{\top} \end{array}\right) \end{aligned} \end{split}\]

Determinant

Definition

The determinant is a scalar value function of a square matrix. The Leibniz formula is

\[ \operatorname{det}(A)=\sum_{\sigma \in S_{n}}\left(\operatorname{sgn}(\sigma) \prod_{i=1}^{n} a_{i, \sigma_{i}}\right) \]

where

  • \(\sigma\) is a permutation of set \({1, 2, \ldots, n}\).

  • \(S_n\) is the set of all such permutations.

  • \(\sigma_i\) is the value in the \(i\)-th position after the reordering \(\sigma\).

  • \(\operatorname{sgn}{\sigma}\) is the signature of \(\sigma\), which is \(1\) if the reordering given by \(\sigma\) can be achieved by successively interchanging two entries an even number of times, and \(-1\) otherwise.

The absolute value of the determinant of a \(2 \times 2\) matrix \(\boldsymbol{A} =[\boldsymbol{a} \quad \boldsymbol{b}] \in \mathbb{R} ^{2 \times 2}\) can be interpreted as the area of parallelogram spanned by the vectors \(\boldsymbol{a}\) and \(\boldsymbol{b}\). The absolute value of the determinant of a \(3 \times 3\) matrix \(\boldsymbol{A} = [\boldsymbol{a} \quad \boldsymbol{b} \quad \boldsymbol{c}] \in \mathbb{R} ^{3 \times 3}\) equals the volume of a parallelepiped spanned by the vectors \(\boldsymbol{a} ,\boldsymbol{b} ,\boldsymbol{c}\). This extends to \(n\)-dimensional parallelotope \(P\): \(\operatorname{det}(\boldsymbol{A}) = \pm \operatorname{vol} (P)\).

Properties

\(\ \)

\[\begin{split} \begin{align} |\boldsymbol{A} \boldsymbol{B}|&=|\boldsymbol{A}||\boldsymbol{B}| \\ \left\vert\begin{array}{l} \boldsymbol{A} \quad \boldsymbol{C} \\ \boldsymbol{0} \quad \boldsymbol{B} \end{array}\right\vert&=| \boldsymbol{A}|| \boldsymbol{B} \mid \\ \left|\boldsymbol{I}_{p}+\boldsymbol{A} \boldsymbol{B}\right|&=\left|\boldsymbol{I}_{q}+\boldsymbol{B} \boldsymbol{A}\right| \end{align} \end{split}\]

Inverse

Definition

The inverse of a square matrix is \(\boldsymbol{A} ^{-1}\) such that \(\boldsymbol{A} \boldsymbol{A} ^{-1} = \boldsymbol{I}\).

Properties

\(\ \)

\[\begin{split} \begin{align} \left(\boldsymbol{A}^{\top}\right)^{-1}&=\left(\boldsymbol{A}^{-1}\right)^{\top} \\ (\boldsymbol{A} \boldsymbol{B})^{-1}&=\boldsymbol{B}^{-1} \boldsymbol{A}^{-1} \\ \left|\boldsymbol{A}^{-1}\right|&=|\boldsymbol{A}|^{-1} \\ (\boldsymbol{A}+\boldsymbol{C B D})^{-1} &=\boldsymbol{A}^{-1}-\boldsymbol{A}^{-1} \boldsymbol{C B}\left(\boldsymbol{B}+\boldsymbol{B D A}^{-1} \boldsymbol{C B}\right)^{-1} \boldsymbol{B D A}^{-1} \\ \left(\boldsymbol{A}+\boldsymbol{c} \boldsymbol{d}^{\top}\right)^{-1}&=\boldsymbol{A}^{-1}-\frac{\boldsymbol{A}^{-1} \boldsymbol{c} \boldsymbol{d}^{\top} \boldsymbol{A}^{-1}}{1+\boldsymbol{d}^{\top} \boldsymbol{A}^{-1} \boldsymbol{c}} \\ \left|\boldsymbol{A}+\boldsymbol{c} \boldsymbol{d}^{\top}\right|&=|\boldsymbol{A}|\left(1+\boldsymbol{d}^{\top} \boldsymbol{A}^{-1} \boldsymbol{c}\right) \end{align} \end{split}\]

If \( \boldsymbol{M}=\left[\begin{array}{cc} \boldsymbol{A} & \boldsymbol{b} \\ \boldsymbol{b}^{\top} & c \end{array}\right] \) Then

\[\begin{split} \boldsymbol{M}^{-1}=\left[\begin{array}{cc} \left(\boldsymbol{A}-\frac{1}{c} \boldsymbol{b} \boldsymbol{b}^{\top}\right)^{-1} & -\frac{1}{k} \boldsymbol{A}^{-1} \boldsymbol{b} \\ -\frac{1}{k} \boldsymbol{b}^{\top} \boldsymbol{A}^{-1} & \frac{1}{k} \end{array}\right]=\left[\begin{array}{cc} \boldsymbol{A}^{-1}+\frac{1}{k} \boldsymbol{A}^{-1} \boldsymbol{b} \boldsymbol{b}^{\top} \boldsymbol{A}^{-1} & -\frac{1}{k} \boldsymbol{A}^{-1} \boldsymbol{b} \\ -\frac{1}{k} \boldsymbol{b}^{\top} \boldsymbol{A}^{-1} & \frac{1}{k} \end{array}\right] \end{split}\]

where \(k = c- \boldsymbol{b} ^\top \boldsymbol{A} ^{-1} \boldsymbol{b}\).

Trace

Definition

For a square matrix \(A\), \(\operatorname{tr}\left( \boldsymbol{A} \right)\) is the sum of the diagonal elements

\[ \operatorname{tr}\left( \boldsymbol{A} \right) = \sum_i a_{ii} \]
Properties

\(\ \)

\[\begin{split}\begin{align} \operatorname{tr}(\boldsymbol{A}+\boldsymbol{B}) &=\operatorname{tr}(\boldsymbol{A})+\operatorname{tr}(\boldsymbol{B}) \\ \operatorname{tr}(\boldsymbol{A B}) &=\operatorname{tr}(\boldsymbol{B} \boldsymbol{A}) \\ \operatorname{tr}(\alpha \boldsymbol{A}) &=\alpha \operatorname{tr}(\boldsymbol{A}) \\ \end{align}\end{split}\]

Eigenvalues and Eigenvectors

If we restricted to \(\lambda \in \mathbb{R}\) then some matrices do not have real eigenvalues.

Definitions

Let \(\boldsymbol{A}\) be an \(n\times n\) square matrix and let \(\boldsymbol{x}\) be an \(n\times 1\) nonzero vector that \(\boldsymbol{A} \boldsymbol{x} = \lambda \boldsymbol{x}\). Then, \(\lambda \in \mathbb{C}\) is called an eigenvalue of \(\boldsymbol{A}\) and \(\boldsymbol{x}\) is called an eigenvector corresponding to eigenvalue \(\lambda\). The eigenvalues are the solutions of the characteristic function

\[ \left\vert \boldsymbol{A} - \lambda \boldsymbol{I} \right\vert = 0 \]

For a fixed \(\lambda\), the non-zero solution \(\boldsymbol{v}\) to \(\boldsymbol{A} \boldsymbol{v} = \lambda \boldsymbol{v}\) is called an eigenvector of \(\boldsymbol{A}\) corresponding to \(\lambda\).

Properties

  • For \(\boldsymbol{A}_{n\times n}\) with eigenvalues \(\lambda_1, \lambda_2, \ldots, \lambda_n\), we have

    • \(\operatorname{tr}(\boldsymbol{A}) =\sum_{i=1}^{n} \lambda_{i}\)

    • \(|\boldsymbol{A}|=\prod_{i=1}^{n} \lambda_{i}\)

    • \(\left|\boldsymbol{I}_{n} \pm \boldsymbol{A}\right|=\prod_{i=1}^{n}\left(1 \pm \lambda_{i}\right)\)

    • if \(\lambda \in \mathbb{R}\) and \(\lambda_1\ge \ldots, \ge \lambda_n\), we say \(\lambda_1\) is the largest (first, top) eigenvalue, and \(\lambda_n\) is the smallest (last, bottom) eigenvalue. Same for corresponding eigenvectors.

  • The nonzero eigenvalues of \(\boldsymbol{A} \boldsymbol{B}\) are the same as those of \(\boldsymbol{B} \boldsymbol{A}\)

  • If \(\boldsymbol{A} + \boldsymbol{B} = \boldsymbol{I}\), and \(\boldsymbol{A}\boldsymbol{v} = \lambda \boldsymbol{v}\), then we can see \(\boldsymbol{B} \boldsymbol{v} = (\boldsymbol{I} - \boldsymbol{A} )\boldsymbol{v} = (1-\lambda)\boldsymbol{v}\).

    • if \(\boldsymbol{A}\) has eigen pairs \((\lambda_i, \boldsymbol{v} _i)\) then \(\boldsymbol{B}\) has eigen pairs \((1-\lambda_i, \boldsymbol{v} _i)\)

    • the sequence of pairs is reversed, e.g. the largest eigenvector of \(\boldsymbol{A}\) is the smallest eigenvector of \(\boldsymbol{B}\).

Uniqueness of eigenvalues and eigenvectors

For an \(N \times N\) square matrix \(\boldsymbol{A}\),

  • Eigenvalues may not be unique. The characteristic function \(p(\lambda)=\operatorname{det}(\boldsymbol{A}-\lambda \boldsymbol{I})=0\) can be written as

    \[ p(\lambda)=\left(\lambda-\lambda_{1}\right)^{n_{1}}\left(\lambda-\lambda_{2}\right)^{n_{2}} \cdots\left(\lambda-\lambda_{N_{\lambda}}\right)^{n_{N_{\lambda}}}=0 \]

    where \(N_\lambda \le N\) is the number of distinct solutions.

    • The integer \(n_i\) is called the algebraic multiplicity of \(\lambda_i\).

    • If the field of scalars is algebraically closed, the algebraic multiplicities sum to \(N\): \(\sum_{i=1}^{N_{\lambda}} n_{i}=N\).

  • For a fixed eigenvalue \(\lambda_i\), the solution to \(\boldsymbol{v}\) to the eigenvalue equation \((\boldsymbol{A} - \lambda_i \boldsymbol{I} )\boldsymbol{v} = \boldsymbol{0}\) is not unique.

    • Any scaling \(c \boldsymbol{v}\) is also an solution.

    • There may be \(m_i\) linearly independent solutions. A linear combinations of the \(m_i\) solutions is also an solution. The number \(m_i\) is called the geometric multiplicity of \(\lambda_i\). We have \(m_i \le n_i\).

    • The total number of linearly independent eigenvectors can be calculated by summing the geometric multiplicities \(\sum_{i=1}^{N_{\lambda}} m_{i}=N_{\boldsymbol{v}} \le N\) with equality iff \(m_i = n_i\) for all \(i\).

    • \(E=\{\boldsymbol{v}:(\boldsymbol{A} -\lambda_i \boldsymbol{I} ) \boldsymbol{v}=\boldsymbol{0}\}\) is called the eigenspace of \(\boldsymbol{A}\) associated with \(\lambda_i\). We have \(\operatorname{dim}(E)=m_i\).

Claims

  • Eigenvectors corresponds to distinct eigenvalues \(\lambda_i \ne \lambda_j\) are independent.

  • Eigenvectors corresponds to the same eigenvalues \(\lambda_i = \lambda_j\) (due to algebraic multiplicity) may or may not be independent.

  • The rank of \(\boldsymbol{A}\) is \(N - \operatorname{dim} (E_0)\), where \(E_0\) is the eigenspace corresponding to eigenvalue \(0\), \(E_0 = \left\{ \boldsymbol{v} : \boldsymbol{A} \boldsymbol{v} = \boldsymbol{0} \right\}\), aka the kernel of \(\boldsymbol{A}\).

    • If \(0\) is not an eigenvalue, then the kernel is trivial, and so the matrix has full rank \(N\).

    • The rank depends on no other eigenvalues.

  • Perron-Frobenius theorem: If \(\boldsymbol{A} \in \mathbb{R} ^{n \times n}\) has all entries positive \(a_{ij} > 0\), then it has a unique largest eigenvalue, and the corresponding eigenvector can be chosen to have all entires positive.

Example: the matrix \(\left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right]\) has

  • one distinct eigenvalue \(0\) with algebraic multiplicity \(2\), i.e. \(N_\lambda=1, n_1 = 2\)

  • all eigenvectors \([c, 0]\) where \(c \ne 0\) are dependent, \(m_1 = 1\).

  • rank 1

For more details see Wikipedia.

Special Matrices

Symmetric Matrices

Definition

A matrix \(\boldsymbol{A}\) is symmetric if \(\boldsymbol{A} ^\top =\boldsymbol{A}\). This is denoted by \(\boldsymbol{A} \in \mathrm{Sym}\).

Orthogonal Matrices

Aka rotation matrices.

Definition

A real square matrix \(\boldsymbol{U}\) is orthogonal if \(\boldsymbol{U} ^{-1} = \boldsymbol{U} ^\top\). Equivalently, if its columns and rows are orthonormal: \(\boldsymbol{U} ^{\top} \boldsymbol{U} = \boldsymbol{U} \boldsymbol{U} ^{\top} = \boldsymbol{I}\).

For instance, \(\boldsymbol{R} =\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\) is a rotation matrix rotates points in the \(xy\)-plane counterclockwise through an angle \(\theta\) with respect to the \(x\) axis about the origin of a two-dimensional Cartesian coordinate system. Given a point \(\boldsymbol{v} = (x, y)\), after rotation its coordinates becomes

\[\begin{split} R \boldsymbol{v} =\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} x \cos \theta-y \sin \theta \\ x \sin \theta+y \cos \theta \end{array}\right] \end{split}\]
Properties

Transformation by \(\boldsymbol{U}\) preserves the length of a vector \(\boldsymbol{x}\), the angle between two vectors \(\boldsymbol{x} , \boldsymbol{y}\).

\[\begin{split}\begin{aligned} \|\boldsymbol{U}\boldsymbol{x} \| &=\|\boldsymbol{x}\| \\ (\boldsymbol{U x})^{\top} \boldsymbol{U} \boldsymbol{y} &=\boldsymbol{x}^{\top} \boldsymbol{y} \end{aligned}\end{split}\]

For a distribution \(f(\boldsymbol{x}; \boldsymbol{\theta})\), rotation \(\boldsymbol{U} ^{\top} \boldsymbol{x}\) preserves its shape, i.e. we can find \(\boldsymbol{\theta} ^\prime\) such that \(f(\boldsymbol{x}; \boldsymbol{\theta}) = f(\boldsymbol{U} ^{\top} \boldsymbol{x}; \boldsymbol{\theta} ^\prime)\), for all \(\boldsymbol{x}\).

Idempotent Matrices

Definition

A matrix \(\boldsymbol{A}\) is idempotent if \(\boldsymbol{A} ^2 = \boldsymbol{A}\).

Properties

If \(\boldsymbol{A}\) is idempotent, then

  • \(\boldsymbol{I} - \boldsymbol{A}\) is also idempotent

  • \(\boldsymbol{U} ^\top \boldsymbol{A} \boldsymbol{U}\) is idempotent if \(\boldsymbol{U}\) is orthogonal

  • \(\boldsymbol{A} ^n = \boldsymbol{A}\) for all positive integer \(n\)

  • it is non-singular iff \(\boldsymbol{A} = \boldsymbol{I}\).

  • has eigenvalues 0 or 1 since \(\lambda \boldsymbol{v} = \boldsymbol{A} \boldsymbol{v} = \boldsymbol{A} ^2 \boldsymbol{v} = \lambda \boldsymbol{A} \boldsymbol{v} = \lambda^2 \boldsymbol{v}\)

  • If \(\boldsymbol{A}\) is also symmetric, then

    • \(\operatorname{rank}\left( \boldsymbol{A} \right) = \operatorname{tr}\left( \boldsymbol{A} \right)\)

    • \(\operatorname{rank}\left( \boldsymbol{A} \right) = r \Rightarrow \boldsymbol{A}\) has \(r\) eigenvalues equal to 1 and \(n-r\) equal to \(0\).

    • \(\operatorname{rank}\left( \boldsymbol{A} \right) = n \Rightarrow \boldsymbol{A} = \boldsymbol{I} _n\)

Reflection Matrices

Definition (Householder reflection)

A Householder transformation (aka Householder reflection) is a linear transformation that describe a reflection about a plane or hyperplane containing the origin. The reflection of a point \(\boldsymbol{x}\) about a hyperplane defined by \(\boldsymbol{v}\) is the linear transformation

\[ \boldsymbol{x} - 2 \langle \boldsymbol{x}, \boldsymbol{v} \rangle \boldsymbol{v} \]

where \(\boldsymbol{v}\) is the unit vector that is orthogonal to the hyperplane.

Definition (Householder matrices)

The matrix constructed from this transformation can be expressed in terms of an outer product as

\[ \boldsymbol{H} = \boldsymbol{I} - 2 \boldsymbol{v} \boldsymbol{v} ^{\top} \]

Properties

  • symmetric: \(\boldsymbol{H} = \boldsymbol{H} ^{\top}\)

  • unitary: \(\boldsymbol{H}^{-1} = \boldsymbol{H} ^{\top}\)

  • involutory: \(\boldsymbol{H}^{-1} = \boldsymbol{H}\)

  • has eigenvalues

    • \(-1\), since \(\boldsymbol{H} \boldsymbol{v} = - \boldsymbol{v}\)

    • \(1\) of multiplicity \(n-1\), since \(\boldsymbol{H} \boldsymbol{u} = \boldsymbol{u}\) where \(\boldsymbol{u} \perp \boldsymbol{v}\), and there are \(n-1\) independent vectors orthogonal to \(\boldsymbol{v}\)

  • has determinant \(-1\).

Projection Matrices

Definition(Projection matrices)

A square matrix \(\boldsymbol{P}\) is called a projection matrix if \(\boldsymbol{P}^2 = \boldsymbol{P}\). By definition, a projection \(\boldsymbol{P}\) is idempotent.

  • If \(P\) is further symmetric, then it is called an orthogonal projection matrix.

  • otherwise it called an oblique projection matrix.

(Orthogonal) Projection

  • onto a line for which \(\boldsymbol{u}\) is a unit vector: \(\boldsymbol{P}_u = \boldsymbol{u} \boldsymbol{u} ^{\top}\)

  • onto a subspace \(\boldsymbol{U}\) with orthonormal basis \(\boldsymbol{u} _1, \ldots, \boldsymbol{u} _k\) forming matrix \(\boldsymbol{A}\): \(\boldsymbol{P}_A = \boldsymbol{A} \boldsymbol{A} ^{\top} = \sum_i \langle \boldsymbol{u} _i, \cdot \rangle \boldsymbol{u} _i\)

  • onto subspace \(\boldsymbol{U}\) with (not necessarily orthonormal) basis \(\boldsymbol{u} _1, \ldots, \boldsymbol{u} _k\) forming matrix \(\boldsymbol{A}\): \(\boldsymbol{P} _{A}= \boldsymbol{A} \left( \boldsymbol{A} ^{\top} \boldsymbol{A} \right) ^{-1} \boldsymbol{A} ^{\top}\). Such as that in linear regression.

Similar Matrices

Two square matrices \(\boldsymbol{A}\) and \(\boldsymbol{B}\) are called similar if there exists an invertible matrix \(\boldsymbol{P}\) such that

\[ \boldsymbol{B} = \boldsymbol{P} ^{-1} \boldsymbol{A} \boldsymbol{P} \]

Similar matrices represent the same linear operator under two (possibly) different bases, with P being the change of basis matrix. As a result, similar matrices share all properties of their shared underlying operator:

  • Rank

  • Characteristic polynomial, and attributes that can be derived from it:

    • Eigenvalues, and their algebraic multiplicities

    • Determinant

    • Trace

  • Geometric multiplicities of eigenvalues (but not the eigenspaces, which are transformed according to the base change matrix P used).

  • Frobenius normal form

  • Jordan normal form, up to a permutation of the Jordan blocks

Besides, \(\boldsymbol{A}\) is called diagonalizable if it is similar to a diagonal matrix.

Positive (Semi-)Definite

Definitions

  • A symmetric matrix \(\boldsymbol{A}\) is positive semi-defiinite (p.s.d.) if \(\boldsymbol{c}^\top \boldsymbol{A} \boldsymbol{c} \ge 0\) for all \(\boldsymbol{c}\). This is denoted by \(\boldsymbol{A} \succ \boldsymbol{0}\) or \(\boldsymbol{A} \in \mathrm{PD}\).

  • A symmetric matrix \(\boldsymbol{A}\) is positive definite (p.d.) if \(\boldsymbol{c}^\top \boldsymbol{A} \boldsymbol{c} \ge 0\) for all \(\boldsymbol{c}\ne \boldsymbol{0}\). This is denoted by \(\boldsymbol{A} \succeq \boldsymbol{0}\) or \(\boldsymbol{A} \in \mathrm{PSD}\).

Properties

\(\ \)

\[\begin{split}\begin{align} \boldsymbol{A} \in \mathrm{PD} &\Leftrightarrow \lambda_i(\boldsymbol{A}) > 0 \\ &\Leftrightarrow \exists \text{ non-singular } \boldsymbol{R}: \boldsymbol{A} = \boldsymbol{R} \boldsymbol{R} ^\top ( \text{Cholesky decomposition} )\\ &\Rightarrow \boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{U} ^{\top} \quad \text{EVD = SVD}\\ &\Rightarrow \boldsymbol{A} ^{-1} = \boldsymbol{U} \boldsymbol{\Lambda} ^{-1} \boldsymbol{U} ^{\top} \text{ where } \operatorname{diag}(\boldsymbol{\Lambda} ^{-1} )=\frac{1}{\lambda_i} \\ &\Rightarrow \exists \boldsymbol{B} = \boldsymbol{U} \boldsymbol{\Lambda}^{1/2} \boldsymbol{U} ^{\top} \in \mathrm{PD}: \boldsymbol{B} ^2 = \boldsymbol{A}, \text{denoted } \boldsymbol{B} = \boldsymbol{A} ^{1/2} = \sqrt{\boldsymbol{A}}\\ &\Rightarrow \sqrt{\boldsymbol{A} ^{-1} } = (\sqrt{\boldsymbol{A} })^{-1},\text{denoted } \boldsymbol{A} ^{-1/2} \\ \boldsymbol{A} \in \mathrm{PSD} &\Leftrightarrow \lambda_i(\boldsymbol{A}) \ge 0 \\ &\Leftrightarrow \exists \text{ square } \boldsymbol{R}, \operatorname{rank}\left( R \right) = \operatorname{rank}\left( \boldsymbol{A} \right): \boldsymbol{A} = \boldsymbol{R} \boldsymbol{R} ^\top\\ &\Rightarrow \exists \boldsymbol{B} = \boldsymbol{U} \boldsymbol{\Lambda}^{1/2} \boldsymbol{U} ^{\top} \in \mathrm{PSD}: \boldsymbol{B} ^2 = \boldsymbol{A} \\ \text{square } \boldsymbol{B} &\Rightarrow \boldsymbol{B} ^\top \boldsymbol{B} \in \mathrm{PSD}\\ \text{any } \boldsymbol{M} \in \mathbb{R} ^{m \times n} &\Rightarrow \boldsymbol{M} \boldsymbol{M} ^\top, \boldsymbol{M} ^{\top} \boldsymbol{M} \in \mathrm{PSD}\\ \end{align}\end{split}\]

Inequalities

  • If \(\boldsymbol{A}\) is p.d., then

    \[ \max _{\boldsymbol{a}} \frac{\left(\boldsymbol{a}^{\top} \boldsymbol{b} \right)^{2}}{\boldsymbol{a}^{\top} \boldsymbol{A} \boldsymbol{a}} \leq \boldsymbol{b} ^{\top} \boldsymbol{A}^{-1} \boldsymbol{b} \]

    The equality holds when \(\boldsymbol{a} \propto \boldsymbol{R} ^{-1} \boldsymbol{b}\). This inequality can be proved by Cauchy-Schwarz inequality \(\left(\boldsymbol{v}^{\top} \boldsymbol{w}\right)^{2} \leq\|\boldsymbol{v}\|^{2}\|\boldsymbol{w}\|^{2}=\left(\boldsymbol{v}^{\top} \boldsymbol{v}\right)\left(\boldsymbol{w}^{\top} \boldsymbol{w}\right)\) where \(\boldsymbol{v} = \boldsymbol{A} ^{1/2} \boldsymbol{a} , \boldsymbol{w} = \boldsymbol{A} ^{-1/2} \boldsymbol{b}\).

  • If \(\boldsymbol{A}\) is symmetric and \(\boldsymbol{B}\) is p.d., both of size \(n \times n\), then for all \(\boldsymbol{a}\) ,

    \[ \lambda_{\min}(\boldsymbol{B} ^{-1} \boldsymbol{A} ) \le \frac{\boldsymbol{a} ^\top \boldsymbol{A} \boldsymbol{a} }{\boldsymbol{a} ^\top \boldsymbol{B} \boldsymbol{a} } \le \lambda_{\max}(\boldsymbol{B} ^{-1} \boldsymbol{A} ) \]

    The equality on either side holds when \(\boldsymbol{a}\) is proportional to the corresponding eigenvector.

  • If \(\boldsymbol{A}\) and \(\boldsymbol{B}\) are p.d.,

    \[ \max _{\boldsymbol{a} , \boldsymbol{b}} \frac{\left(\boldsymbol{a}^{\top} \boldsymbol{D} \boldsymbol{b}\right)^{2}}{\boldsymbol{a}^{\top} \boldsymbol{A} \boldsymbol{a} \cdot \boldsymbol{b}^{\top} \boldsymbol{B} \boldsymbol{b}}=\theta \]

    where \(\theta\) is the largest eigenvalue of \(\boldsymbol{A} ^{-1} \boldsymbol{D} \boldsymbol{B} ^{-1} \boldsymbol{D} ^\top\) or \(\boldsymbol{B} ^{-1} \boldsymbol{D} ^\top \boldsymbol{A} ^{-1} \boldsymbol{D}\).

    The maximum is obtained when \(\boldsymbol{a}\) is proportional to an eigenvector of \(\boldsymbol{A} ^{-1} \boldsymbol{D} \boldsymbol{B} ^{-1} \boldsymbol{D} ^\top\) corresponding to \(\theta\), \(\boldsymbol{b}\) is proportional to an eigenvector of \(\boldsymbol{B} ^{-1} \boldsymbol{D} ^\top \boldsymbol{A} ^{-1} \boldsymbol{D}\) corresponding to \(\theta\).

  • If \(\boldsymbol{A} , \boldsymbol{\Sigma}\) are p.d., then the function

    \[ f(\boldsymbol{\Sigma} ) = \log \left\vert \boldsymbol{\Sigma} \right\vert + \operatorname{tr}\left( \boldsymbol{\Sigma} ^{-1} \boldsymbol{A} \right) \]

    is minimized uniquely at \(\boldsymbol{\Sigma} =\boldsymbol{A}\). This is used in the derivation of MLE for multivariate Gaussian.

Conditional Negative Definite

Definition (Conditionally negative definite)

A symmetric matrix \(\boldsymbol{A}\) is called conditionally negative definite (c.n.d.) if \(\boldsymbol{c}^{\top} \boldsymbol{A} \boldsymbol{c} \le 0\) for all \(\boldsymbol{c}:\boldsymbol{1} ^{\top} \boldsymbol{c} = 0\).

Theorem (Schoenberg)

A symmetric matrix \(\boldsymbol{A}\) with zero diagonal entires is c.n.d. if and only if it can be realized as the square of the mutual Euclidean distance between points: \(a_{ij} = \left\| \boldsymbol{x}_i - \boldsymbol{x}_j \right\|\) for \(i, j= 1, \ldots, n\) and some \(\boldsymbol{x}_i \in \mathbb{R} ^d\).

Matrix Decomposition

Summary table

Spectral Decomposition

Aka eigendecomposition.

For discussion of uniqueness and independence of eigenvectors, see previous section.

If a square matrix \(\boldsymbol{A}\) has \(n\) independent eigenvectors, then it can be written as \(\boldsymbol{A} = \boldsymbol{U} \boldsymbol{A} \boldsymbol{U} ^{-1}\). The columns in the matrix \(\boldsymbol{U}\) are the eigenvectors of \(\boldsymbol{A}\) and \(\boldsymbol{\Lambda}\) is a diagonal matrix of eigenvalues. We say \(\boldsymbol{A}\) has eigendecomposition (EVD), and is diagonalizable.

In particular, if \(\boldsymbol{A}\) is symmetric, then \(\boldsymbol{U}\) is a orthogonal matrix, and hence \(\boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{U} ^{\top}\). Moreover, \(\lambda\) are all real.

Proof

Suppose that \((\lambda, \boldsymbol{v})\) is a (possibly complex) eigenvalue and eigenvector pair of the a symmetric matrix \(\boldsymbol{A}\). Using the fact that \(\overline{\boldsymbol{A} \boldsymbol{v}} = \overline{\lambda \boldsymbol{v}} \Rightarrow \boldsymbol{A} \overline{\boldsymbol{v}} = \overline{\lambda} \overline{\boldsymbol{v}}\) and \(\boldsymbol{A} ^{\top} = \boldsymbol{A}\), we have

\[\begin{split} \begin{aligned} \overline{\boldsymbol{v}}^{\top} \boldsymbol{A} \boldsymbol{v}=\overline{\boldsymbol{v}}^{\top}(\boldsymbol{A} \boldsymbol{v})=\overline{\boldsymbol{v}}^{\top}(\lambda \boldsymbol{v})=\lambda(\overline{\boldsymbol{v}} \cdot \boldsymbol{v}) \\ \overline{\boldsymbol{v}}^{\top} \boldsymbol{A} \boldsymbol{v}=(\boldsymbol{A} \overline{\boldsymbol{v}})^{\top} \boldsymbol{v}=(\bar{\lambda} \overline{\boldsymbol{v}})^{\top} \boldsymbol{v}=\bar{\lambda}(\overline{\boldsymbol{v}} \cdot \boldsymbol{v}) \end{aligned} \end{split}\]

Since \(\boldsymbol{v} \neq \boldsymbol{0}\), we have \(\overline{\boldsymbol{v}} \cdot \boldsymbol{v} \neq 0\). Thus \(\lambda=\bar{\lambda}\), which means \(\lambda \in \mathbb{R}\).

We can write

\[ \boldsymbol{A} = \sum_{i=1}^n \lambda_i \boldsymbol{u} _i \boldsymbol{u} _i ^{\top} \]

Let \(\boldsymbol{P}_i = \boldsymbol{u} _i \boldsymbol{u} _i ^{\top}\), then

  • \(\boldsymbol{P}_i\) is an orthogonal projection matrix (or projector) to the \(1\)-dimensional eigenspace \(\left\{ c \boldsymbol{u} _i \right\}\)

  • \(\boldsymbol{P} _i\) is idempotent: \(\boldsymbol{P}_i \boldsymbol{P} _i = \boldsymbol{P} _i\)

  • its complementary \(\boldsymbol{I} - \boldsymbol{P}_i\) is a projector to \(\left\{ c \boldsymbol{u} _i \right\} ^\bot\).

Cholesky Decomposition

If \(\boldsymbol{A}\) is p.s.d. (p.d.), there exists a (unique) upper triangular matrix \(\boldsymbol{U}\) with non-negative (positive) diagonal elements such that

\[ \boldsymbol{A} = \boldsymbol{U} ^\top \boldsymbol{U} \]

Cholesky decomposition is a special case of LU decomposition.

Canonical Decomposition

If \(\boldsymbol{A}\) is symmetric and \(\boldsymbol{B}\) is p.d., then there exists a non-singular matrix \(\boldsymbol{P}\) such that

\[\boldsymbol{P} ^\top \boldsymbol{A} \boldsymbol{P} = \boldsymbol{\Lambda} \text{ and } \boldsymbol{P} ^\top \boldsymbol{B} \boldsymbol{P} = \boldsymbol{I} _n\]

where \(\boldsymbol{\Lambda} =\operatorname{diag}\left( \lambda_1, \lambda_2, \ldots, \lambda_n \right)\) and the \(\lambda_i\) are the eigenvalues of \(\boldsymbol{B} ^{-1} \boldsymbol{A}\) or \(\boldsymbol{A} \boldsymbol{B} ^{-1}\).

Singular Value Decomposition

Definition

For any matrix \(\boldsymbol{A} \in \mathbb{R} ^{n \times p}\), we can write \(\boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V} ^\top\). where

  • \(\boldsymbol{U} \in \mathbb{R} ^{n \times n}\) and \(\boldsymbol{V} \in \mathbb{R} ^{p\times p}\) are orthogonal matrices.

  • \(\boldsymbol{\Sigma}\) is an \(n \times p\) matrix, where the diagonal entires are singular values \(\sigma_{ii} > 0\) for \(i = 1, 2, \ldots, r\), where \(r = \operatorname{rank}(\boldsymbol{A})\).

Properties

  • Due to the definition of \(\boldsymbol{\Sigma}\), we can write SVD as

    \[ \boldsymbol{A}=\sigma_{1} \boldsymbol{u}_{1} \boldsymbol{v}_{1}^{\top}+\sigma_{2} \boldsymbol{u}_{2} \boldsymbol{v}_{2}^{\top}+\ldots+\sigma_{r} \boldsymbol{u}_{r} \boldsymbol{v}_{r}^{\top} = \tilde{\boldsymbol{U}}_{n \times r} \tilde{\boldsymbol{\Sigma}} _{r \times r} \tilde{\boldsymbol{V}}_{r \times r} \]

    where \(r = \operatorname{rank}\left( \boldsymbol{A} \right)\). It is then easy to see that \(\boldsymbol{A} \boldsymbol{v}=\sigma \boldsymbol{u}, \boldsymbol{A}^{\top} \boldsymbol{u}=\sigma \boldsymbol{v}\).

  • When \(\boldsymbol{A}\) is symmetric, then its SVD \(\boldsymbol{A} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V} ^{\top}\) can be obtained from its EVD:

    \[\boldsymbol{A} = \boldsymbol{W} \boldsymbol{\Lambda} \boldsymbol{W} ^{\top} = \sum_{i=1}^n \lambda_i \boldsymbol{w} _i \boldsymbol{w}_i ^{\top} = \sum_{i=1}^r \underbrace{\left\vert \lambda_i \right\vert }_{\sigma_i} \underbrace{\operatorname{sign}(\lambda_i) \boldsymbol{w} _i \boldsymbol{w} _i ^{\top}}_{\boldsymbol{u} _i \boldsymbol{v} _i ^{\top}}\]

    For instance, we can let \(\boldsymbol{u} _i = \operatorname{sign}(\lambda_i) \boldsymbol{w} _i\) and \(\boldsymbol{v} _i = \boldsymbol{w} _i\), or \(\boldsymbol{u} _i = - \boldsymbol{w} _i\) and \(\boldsymbol{v} _i = - \operatorname{sign}(\lambda_i) \boldsymbol{w}_i\), etc. Note that when \(\lambda_\max > 0\), we may not have \(\sigma_\max = \lambda_\max\), but we always have \(\sigma_\max \ge \lambda_\max\).

Theorem

Every matrix has SVD.

QR Decomposition

LU Decomposition

Schur Decomposition

More Topics

Matrix Differentiation

Definitions

\(\ \)

\[\begin{split} \begin{array}{l} \frac{\partial y}{\partial \boldsymbol{x}}=\left(\begin{array}{c} \frac{\partial y}{\partial x_{1}} \\ \vdots \\ \frac{\partial y}{\partial x_{n}} \end{array}\right) \\ \frac{\partial y}{\partial \boldsymbol{X}}=\left(\begin{array}{ccc} \frac{\partial y}{\partial x_{11}} & \cdots & \frac{\partial y}{\partial x_{1 n}} \\ \vdots & & \vdots \\ \frac{\partial y}{\partial x_{n 1}} & \cdots & \frac{\partial y}{\partial x_{n n}} \end{array}\right) \end{array} \end{split}\]
Properties

\(\ \)

\[\begin{split} \begin{aligned} \frac{\partial \boldsymbol{a}^{\top} \boldsymbol{x}}{\partial \boldsymbol{x}}&=\boldsymbol{a}\\ \frac{\partial \boldsymbol{A} \boldsymbol{x}}{\partial \boldsymbol{x}}&=\boldsymbol{A}\\ \frac{\partial \boldsymbol{x}^{\top} \boldsymbol{A} \boldsymbol{x}}{\partial \boldsymbol{x}}&=\boldsymbol{A} ^{\top} \boldsymbol{x} + \boldsymbol{A} \boldsymbol{x} \\ &=2 \boldsymbol{A} \boldsymbol{x} \text { if } \boldsymbol{A} \text { is symmetric. }\\ \frac{\partial \operatorname{tr}(\boldsymbol{X})}{\partial \boldsymbol{X}}&=\boldsymbol{I}\\ \frac{\partial \operatorname{tr}(\boldsymbol{A} \boldsymbol{X})}{\partial \boldsymbol{X}}&=\left\{\begin{array}{ll} \boldsymbol{A}^{\top} &\text { if all elements of } \boldsymbol{X} \text { are distinct } \\ \boldsymbol{A}+\boldsymbol{A}^{\top}-\operatorname{diag}(\boldsymbol{A}) &\text { if } \boldsymbol{X} \text { is symmetric. } \end{array}\right.\\ \frac{\partial|\boldsymbol{X}|}{\partial \boldsymbol{X}}&=\left\{\begin{array}{ll} |\boldsymbol{X}|\left(\boldsymbol{X}^{-1}\right)^{\top} &\text { if all elements of } \boldsymbol{X} \text { are distinct } \\ |\boldsymbol{X}|\left(2 \boldsymbol{X}^{-1}-\operatorname{diag}\left(\boldsymbol{X}^{-1}\right)\right)^{\top} &\text { if } \boldsymbol{X} \text { is symmetric. } \end{array}\right. \end{aligned} \end{split}\]

Vector Norms

  • For \(\boldsymbol{a} , \boldsymbol{b} \in [m]^d\)

    \[ \|\boldsymbol{a}-\boldsymbol{b}\|_{\infty} \leq\|\boldsymbol{a}-\boldsymbol{b}\|_{2} \leq\|\boldsymbol{a}-\boldsymbol{b}\|_{1} \leq \sqrt{d}\|\boldsymbol{a}-\boldsymbol{b}\|_{2} \leq d\|\boldsymbol{a}-\boldsymbol{b}\|_{\infty} \]

Fig. 8 Vector norms [Wang 2021]

Matrix Norms

Reference link

Let \(\boldsymbol{A} \in \mathbb{R} ^{n \times m}\).

  • Frobenius Norm link

  • Infinity norm: maximum row sum of absolute entires

    \[\|A\|_{\infty}=\max _{1 \leq i \leq n}\left(\sum_{j=1}^{m}\left|a_{i j}\right|\right)\]

  • 1-norm: maximum column sum of absolute entires

    \[\|A\|_{1}=\max _{1 \leq j \leq m}\left(\sum_{i=1}^{n}\left|a_{i j}\right|\right)\]

  • Spectral norm: \(\left\| \boldsymbol{A} \right\| _2\) is the largest singular value of \(\boldsymbol{A}\).

    • Equals the square root of the largest eigenvalue of \(\boldsymbol{A} ^{\top} \boldsymbol{A}\)

    • Equals \(\lambda_{\max}(\boldsymbol{A})\) if \(\boldsymbol{A}\) is p.s.d.

    • If \(\left\| \boldsymbol{u} \right\| =1, \left\| \boldsymbol{v} \right\| =1\), let \(\boldsymbol{A} = \boldsymbol{u} \boldsymbol{u} ^{\top} - \boldsymbol{v} \boldsymbol{v} ^{\top}\), then \(\left\| \boldsymbol{A} \right\| _2 = \sin \theta\), where \(\theta\) is the angle between \(\boldsymbol{u}\) and \(\boldsymbol{v}\).

      • To prove this, let \(\alpha = \boldsymbol{u} ^{\top} \boldsymbol{v}\). It is easy to verify that \(\boldsymbol{u}\), \(\boldsymbol{v}\) are two eigenvectors of \(\boldsymbol{A} ^{\top} \boldsymbol{A}\) with the same eigenvalue \(1 - \alpha^2\). Hence \(\left\| \boldsymbol{A} \right\| _2 ^2 = 1 - \alpha^2 = 1 - \cos^2\theta\).

Johnson-Lindenstrauss Lemma

Lemma (Johnson-Lindenstrauss)

For data vectors be \(\boldsymbol{x} _1, \boldsymbol{x} _2, \ldots, \boldsymbol{x} _n \in \mathbb{R} ^d\) and tolerance \(\epsilon \in (0, \frac{1}{2} )\), there exists a Lipschitz mapping \(f: \mathbb{R} ^d \rightarrow \mathbb{R} ^k\), where \(k = \lfloor \frac{24 \log n}{\epsilon^2} \rfloor\) such that

\[ (1 - \epsilon) \left\| \boldsymbol{x}_i - \boldsymbol{x}_j \right\| ^2 \le \left\| f(\boldsymbol{x}_i ) - f(\boldsymbol{x}_j )\right\| \le (1 + \epsilon) \left\| \boldsymbol{x}_i - \boldsymbol{x}_j \right\| ^2 \]

How do we construct \(f\)? Consider a random linear mapping: \(f(\boldsymbol{u}) = \frac{1}{\sqrt{k}} \boldsymbol{A} \boldsymbol{u}\) for some \(\boldsymbol{A} \in \mathbb{R} ^{k \times d}\) where \(k < d\) and \(a_{ij} \overset{\text{iid}}{\sim} \mathcal{N} (0, 1)\). The intuition: the columns of \(\boldsymbol{A}\) are orthogonal to each other in expectation. If indeed orthogonal, then \(\left\| \frac{1}{\sqrt{k}} \boldsymbol{A} \boldsymbol{u} \right\| = \left\| \boldsymbol{u} \right\|\).

To prove it, we need the following lemma.

Lemma (Norm preserving)

Fix a vector \(\boldsymbol{u} \in \mathbb{R} ^d\), then \(\boldsymbol{A}\) preserves its norm in expectation.

\[ \mathbb{E} \left[ \left\| \frac{1}{\sqrt{k}} \boldsymbol{A} \boldsymbol{u} \right\|^2 \right] = \mathbb{E} [\left\| \boldsymbol{u} \right\|^2] \]

Proof

\[\begin{split}\begin{aligned} \frac{1}{k} \mathbb{E} [\left\| \boldsymbol{A} \boldsymbol{u} \right\| ^2] &= \frac{1}{k} \boldsymbol{u} ^{\top} \mathbb{E} [\boldsymbol{A} ^{\top} \boldsymbol{A} ] \boldsymbol{u} \\ &= \frac{1}{k} \boldsymbol{u} ^{\top} k \boldsymbol{I}_{n \times n} \boldsymbol{u} \\ &= \left\| \boldsymbol{u} \right\| ^2 \\ \end{aligned}\end{split}\]

The second equality holds since

\[\begin{split} \mathbb{E} [\boldsymbol{a} _i ^{\top} \boldsymbol{a} _j] = \left\{\begin{array}{ll} \sum_{p=1}^k \mathbb{E} [a_{ik}^2] = \sum_{p=1}^k 1 =k , & \text { if } i=j \\ 0, & \text { otherwise } \end{array}\right. \end{split}\]
Lemma (Concentration)

Blessing of high dimensionality: things concentrate around mean. The probability of deviation is bounded. We first prove one-side deviation probability. The proof for the other side is similar.

\[ \mathbb{P} \left( \left\| \frac{1}{\sqrt{k}} \boldsymbol{A} \boldsymbol{u} \right\| ^2 > (1 + \epsilon) \left\| \boldsymbol{u} \right\| ^2 \right) \le \exp \left( \frac{k}{2} \left( \frac{\epsilon^2}{2} - \frac{\epsilon^3}{2} \right) \right) \]

Proof

Let \(\boldsymbol{v} = \frac{\boldsymbol{A} \boldsymbol{u} }{\left\| \boldsymbol{u} \right\| } \in \mathbb{R} ^k\), it is easy to see \(V_i \sim \mathcal{N} (0, 1)\). In this case,

\[\begin{split}\begin{aligned} \mathbb{P}\left( \left\| \boldsymbol{v} \right\| ^2 > (1 + \epsilon) k\right) &= \mathbb{P}\left( \exp (\lambda \left\| \boldsymbol{v} \right\| ^2) > \exp (1+ \epsilon) k \lambda \right) \\ &\le \frac{\mathbb{E} [\exp (\lambda \left\| \boldsymbol{v} \right\| ^2)] }{\exp [ (1+ \epsilon) k\lambda]} \quad \because \text{Markov inequality} \\ &\le \frac{[\mathbb{E} [\exp (\lambda V_i^2)]]^k }{\exp [ (1+ \epsilon) k\lambda]} \quad \because V_i \text{ are i.i.d.} \\ &= \exp [-(1 + \epsilon) k \lambda] \left( \frac{1}{1-2\lambda} \right)^{k/2} \\ \end{aligned}\end{split}\]

The last equality holds since by moment generating function \(\mathbb{E} [e^{tX}] = \frac{1}{\sqrt{1- 2t} }\) for \(X \sim \chi ^2 _1\).

If we choose \(\lambda = \frac{\epsilon}{2(1+\epsilon)} < \frac{1}{2}\), then

\[ \mathbb{P} (\left\| \boldsymbol{v} \right\| > (1 + \epsilon)k) \le \left[ (1+\epsilon)e^{- \epsilon} \right]^{k/2}. \]

Then it remains to show \(1+\epsilon \le \exp(\epsilon - \frac{\epsilon^2}{2} + \frac{\epsilon^3}{2})\) for \(\epsilon > 0\), which is true by derivative test. Plug in this inequality we get the required inequality.

Then by union bound,

\[ \mathbb{P}\left( \left\| \boldsymbol{v} \right\| > (1 + \epsilon) k \text{ or } \left\| \boldsymbol{v} \right\| < (1 - \epsilon) k \right) \le 2 \exp \left(\frac{k}{2}\left(\frac{\epsilon^{2}}{2}-\frac{\epsilon^{3}}{2}\right)\right) \]

Now we prove the JL lemma.

Proof of JL

The probability we fail to find an \(\epsilon\)-distortion map for any \((i, j)\) pair is

\[\begin{split}\begin{aligned} &= \mathbb{P} \left( \exists i, j: \left\| \boldsymbol{A} \boldsymbol{x}_i - \boldsymbol{A} \boldsymbol{x}_j \right\|^2 > (1 + \epsilon) \left\| \boldsymbol{x}_i - \boldsymbol{x}_j \right\| ^2 \text{ or } < (1 - \epsilon) \left\| \boldsymbol{x}_i - \boldsymbol{x}_j \right\| ^2 \right) \\ &= \mathbb{P} \left( \cup_{(i,j)} \right) \\ &\le \binom{n}{2} 2 \exp \left(\frac{k}{2}\left(\frac{\epsilon^{2}}{2}-\frac{\epsilon^{3}}{2}\right)\right)\quad \because \text{union bound} \\ &\le 2 n^2 \exp \left(\frac{k}{2}\left(\frac{\epsilon^{2}}{2}-\frac{\epsilon^{3}}{2}\right)\right)\\ \end{aligned}\end{split}\]

With some choice of \(k\), this upper bound is \(1 - \frac{1}{n}\), i.e. there is an \(\frac{1}{n}\) chance we get a map with \(\epsilon\) distortion. What if we want a higher probability?

For some \(\alpha\), if we set, \(k \ge (4 + 2\alpha) \left( \frac{\epsilon^{2}}{2}-\frac{\epsilon^{3}}{2} \right) ^{-1} \log(n)\), then the embedding \(f(\boldsymbol{x} ) = \frac{1}{\sqrt{k}} \boldsymbol{A} \boldsymbol{x}\) succeeds with probability at least \(1 - \frac{1}{n^\alpha}\).

Low-rank Approximation

Problem:

\[ \min _{\widehat{\boldsymbol{A}}} \quad\|\boldsymbol{A}-\widehat{\boldsymbol{A}}\|_{F} \quad \text { s.t. } \quad \operatorname{rank}(\widehat{\boldsymbol{A}}) \leq r \]

Eckart–Young–Mirsky theorem: We claim that the best rank \(r\) approximation to \(\boldsymbol{A}\) in the Frobenius norm, denoted by \(\boldsymbol{A}_{r}=\sum_{i=1}^{k} \sigma_{i} u_{i} v_{i}^{\top}\). The minimum equals

\[ \left\|\boldsymbol{A}-\boldsymbol{A}_{r}\right\|_{F}^{2}=\left\| \sum_{i=r+1}^{n} \sigma_{i} u_{i} v_{i}^{\top} \right\| _{F}^{2}=\sum_{i=r+1}^{n} \sigma_{i}^{2} \]

Perturbation and Davis-Kahan Theorem

Reference

Suppose we want to recover the top \(r\) subspace of symmetric matrix \(\boldsymbol{M}\) via \(\hat{\boldsymbol{M}} = \boldsymbol{M} + \boldsymbol{H}\), where \(\boldsymbol{H}\) is some small perturbation. Let their spectral decomposition be

\[\begin{split}\begin{aligned} \boldsymbol{M} &= [\boldsymbol{U} _0 \ \boldsymbol{U} _1] \left[\begin{array}{cc} \boldsymbol{\Lambda} _0 & 0 \\ 0 & \boldsymbol{\Lambda} _1 \end{array}\right] \left[\begin{array}{c} \boldsymbol{U} _0 ^{\top} \\ \boldsymbol{U} _1 ^{\top} \end{array}\right] \\ \widehat{\boldsymbol{M}} &= [\widehat{\boldsymbol{U}} _0 \ \widehat{\boldsymbol{U}} _1] \left[\begin{array}{cc} \widehat{\boldsymbol{\Lambda}} _0 & 0 \\ 0 & \widehat{\boldsymbol{\Lambda}} _1 \end{array}\right] \left[\begin{array}{c} \widehat{\boldsymbol{U}} _0 ^{\top} \\ \widehat{\boldsymbol{U}} _1 ^{\top} \end{array}\right] \end{aligned}\end{split}\]

where the partition is at \(r\).

We need a distance measure between subspaces \(\boldsymbol{U} _0\) and \(\widehat{\boldsymbol{U} }_0\), or in general, distance measure between two orthogonal matrices \(\boldsymbol{X} = [\boldsymbol{X} _0 \ \boldsymbol{X} _1]\) and \(\boldsymbol{Z} = [\boldsymbol{Z} _0 \ \boldsymbol{Z} _1]\). All norms below are spectral norms (maximum singular value of a matrix).

  • bad idea: \(\operatorname{dist}(\boldsymbol{X} _0, \boldsymbol{Z} _0) = \left\| \boldsymbol{X} _0 - \boldsymbol{Z} _0 \right\|_2\)

    • \(\boldsymbol{Z} _0\) and \(\boldsymbol{Z} _0 \boldsymbol{Q}\) spans the same column space (rotation of bases) for all orthogonal transformation \(\boldsymbol{Q}\)

    • after rotation, distance changes, not a good measure.

  • good idea: \(\operatorname{dist}(\boldsymbol{X} _0, \boldsymbol{Z} _0) = \left\| \boldsymbol{X} _0 \boldsymbol{X} _0 ^{\top} - \boldsymbol{Z} _0 \boldsymbol{Z} _0 ^{\top} \right\|_2\)

    • invariant to rotation transformation

    • essentially compare projection

Lemmas (of the good idea)

  1. The SVD of \(\boldsymbol{X} _0 ^{\top} \boldsymbol{Z} _0\) can be expressed as \(\boldsymbol{U} \cos (\Theta) \boldsymbol{V} ^{\top}\) where \(\Theta = \operatorname{diag} (\theta_1, \ldots, \theta_r)\) is called the principal angles between two subspaces. (think about \(r=1\) case). We have

\[\left\| X_0 ^{\top} \boldsymbol{Z} _1 \right\| = \left\| \sin \Theta \right\| = \max \left\{ |\sin \theta_1|, \ldots, |\sin \theta_r |\right\}\]

  1. \(\operatorname{dist}(\boldsymbol{X} _0, \boldsymbol{Z} _0) = \left\| \boldsymbol{X} ^{\top} _0 \boldsymbol{Z} _1\right\| = \left\| \boldsymbol{Z} _0 ^{\top} \boldsymbol{X} _1 \right\|\)

    • in particular, if \(\boldsymbol{X} _0 = \boldsymbol{Z} _0\), then the distance measure should be \(0\), and the RHS is indeed 0.

Example of Lemma 1

Think about a simple case in \(2\)-d: \(\boldsymbol{X} = \frac{1}{\sqrt{2}} \left[\begin{array}{cc} 1 & -1 \\ 1 & 1 \end{array}\right]\) and \(\boldsymbol{Z} = \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]\), then

  • \(\cos \theta_{( \boldsymbol{x} _0, \boldsymbol{z} _0 )} = \cos(\theta_1 = \frac{\pi}{4} ) = \boldsymbol{x} _0 ^{\top} \boldsymbol{z} _0\)

  • \(\cos \theta_{(\boldsymbol{x} _0, \boldsymbol{z} _1 )} = \cos(\frac{\pi}{2} - \theta_1 ) = \sin(\theta_1) = \boldsymbol{x} _0 ^{\top} \boldsymbol{z} _1\).

Proof

Lemma 1

\[\begin{split}\begin{aligned} \left\| \boldsymbol{X} _0 ^{\top} \boldsymbol{Z} _1 \right\| &= \left\| \boldsymbol{X} _0 ^{\top} \boldsymbol{Z} _1 \boldsymbol{Z} _1 ^{\top} \boldsymbol{X} _0 \right\|^{1/2} \quad \because \text{SVD} \\ &= \left\| \boldsymbol{X} _0 (\boldsymbol{I} - \boldsymbol{Z} _0 \boldsymbol{Z} _0 ^{\top} ) \boldsymbol{X} _0 \right\|^{1/2} \\ &= \left\| \boldsymbol{I} _{r} - \boldsymbol{X} _0 ^{\top} \boldsymbol{Z} _0 \boldsymbol{Z} _0 ^{\top} \boldsymbol{X} _0 \right\|^{1/2} \\ &= \left\| \boldsymbol{I} _{r} - \boldsymbol{U} [\cos \boldsymbol{\Theta}]^2 \boldsymbol{U} ^{\top} \right\|^{1/2} \\ &= \left\| [\sin \boldsymbol{\Theta}]^2 \right\|^{1/2} \\ &= \left\| \sin \boldsymbol{\Theta} \right\|\\ \end{aligned}\end{split}\]

Lemma 2

By Lemma 1, it remains to show \(\left\| \boldsymbol{X} _0 \boldsymbol{X} _0 ^{\top} - \boldsymbol{Z} _0 \boldsymbol{Z} _0 ^{\top} \right\| = \left\| \sin \boldsymbol{\Theta} \right\|\). Write

\[\begin{split}\boldsymbol{Z} _0 = \boldsymbol{X} \boldsymbol{X} ^{\top} \boldsymbol{Z} _0 = \boldsymbol{X} \left[\begin{array}{cc} \boldsymbol{X} _0 ^{\top} \\ \boldsymbol{X} _1 ^{\top} \end{array}\right] \boldsymbol{Z} _0 = \boldsymbol{X} \left[\begin{array}{cc} \boldsymbol{U} \cos(\boldsymbol{\Theta} ) \boldsymbol{V} ^{\top} \\ \boldsymbol{\tilde{U}} \sin(\boldsymbol{\Theta} ) \boldsymbol{V} ^{\top} \end{array}\right] \end{split}\]

…

Theorem (Davis-Kahan \(\sin(\boldsymbol{\Theta} )\))

If there exists \(a\) and \(\Delta >0\) such that \(\lambda_r(\boldsymbol{M}) \ge a\) and \(a - \Delta \ge \lambda_{r+1} (\widehat{\boldsymbol{M}})\), i.e. the two eigenvalues are at least \(\Delta\) apart, then the perturbation error to subspaces is bounded by

\[ \left\| \boldsymbol{U}_0 \boldsymbol{U} _0 ^{\top} - \boldsymbol{\widehat{U}}_0 \boldsymbol{\widehat{U}} _0 ^{\top} \right\| = \left\| \sin \boldsymbol{\Theta} \right\| \le \frac{\left\| \boldsymbol{H} \boldsymbol{U} _0\right\| }{\Delta} \le \frac{\left\| \boldsymbol{H} \right\| }{\Delta} \]

The \(\Delta\) term in the bound involves eigenvalues of \(\boldsymbol{M}\) and \(\widehat{\boldsymbol{M}}\), can we simplify that? By Weyl’s inequality \(\left\vert \lambda_i(\boldsymbol{M} ) - \lambda_i (\widehat{\boldsymbol{M}})\right\vert \le \left\| \boldsymbol{H} \right\|\). Therefore, we can let

\[\Delta = \lambda_r(\boldsymbol{M} ) - \lambda_{r+1} (\widehat{\boldsymbol{M}}) \ge \lambda_r(\boldsymbol{M} ) - \lambda_{r+1} (\boldsymbol{M} ) - \left\| \boldsymbol{H} \right\| \]

and hence the bound becomes

\[ \operatorname{dist}(\boldsymbol{U} _0, \boldsymbol{\widehat{\boldsymbol{U}}} _0) \le \frac{\left\| H \right\| }{\lambda_r(\boldsymbol{M} ) - \lambda_{r+1} (\boldsymbol{M} ) - \left\| \boldsymbol{H} \right\|} \]

where \(\lambda_r(\boldsymbol{M} ) - \lambda_{r+1} (\boldsymbol{M} )\) is the spectral gap between the \(r\)-th and the \((r+1)\)-th eigenvalues. We can see that the bound is smaller if there is a sharp gap, and increases as noise \(\left\| \boldsymbol{H} \right\|\) increases.

More topics

  • Wigner semicircle distribution of eigenvalues of a random Gaussian matrix Wikipedia

Marchenko–Pastur Distribution

The distribution describe the spectrum of \(\hat{\boldsymbol{\Sigma}}\), i.e. the limiting histogram of its \(p\) eigenvalues as \(p,n \rightarrow \infty\).

If \(\boldsymbol{x}_i \sim \mathcal{N} (\boldsymbol{0} , \boldsymbol{I} _p)\), then the eigenvalues of the (biased) sample covariance matrix \(\hat{\boldsymbol{\Sigma}}= \frac{1}{n} \boldsymbol{X} ^{\top} \boldsymbol{X}\), as \(p, n \rightarrow \infty\), follows Marchenko–Pastur distribution parameterized by \(\gamma = \lim _{n, p \rightarrow \infty} \frac{p}{n}\),

\[\begin{split} \mu^{M P}(t)=\left(1-\frac{1}{\gamma}\right) \delta(t) \mathbb{I} \left\{ \gamma>1 \right\}+\left\{\begin{array}{ll} 0 & t \notin[\gamma_{-}, \gamma_{+}], \\ \frac{\sqrt{(\gamma_{+}-t)(t-\gamma_{-})}}{2 \pi \gamma t} \mathrm{~d} t & t \in[\gamma_{-}, \gamma_{+}], \end{array}\right. \end{split}\]

  • \(\gamma_{\pm} = (1 \pm \sqrt{\gamma})^2\)

  • If \(\gamma \le 1\), the distribution has a support on \([\gamma_{-}, \gamma_{+}]\)

  • If \(\gamma > 1\), it has an additional point mass \(1 - \gamma ^{-1}\) at the origin.

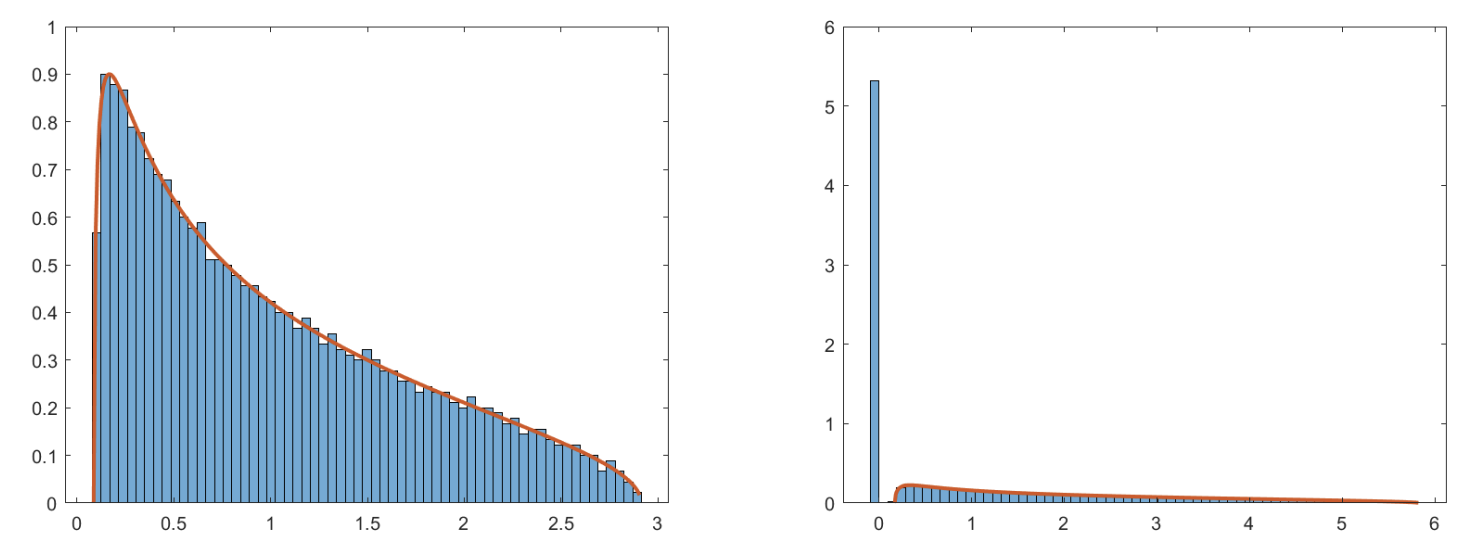
Fig. 9 Marchenko-Pastur distribution with \(\gamma=1/2\) (left, \(d=2000, n=4000\)) and \(\gamma = 0.5\) (right, \(d=8000, n=4000\), with a point mass at origin). [Li & Yi 2021]

Note that when \(p\) is fixed and sample size \(n\) increases, \(\gamma \rightarrow 0\), the interval \(\left[\gamma_{-}, \gamma_{+}\right]\) is tighter, i.e. more concentrated.

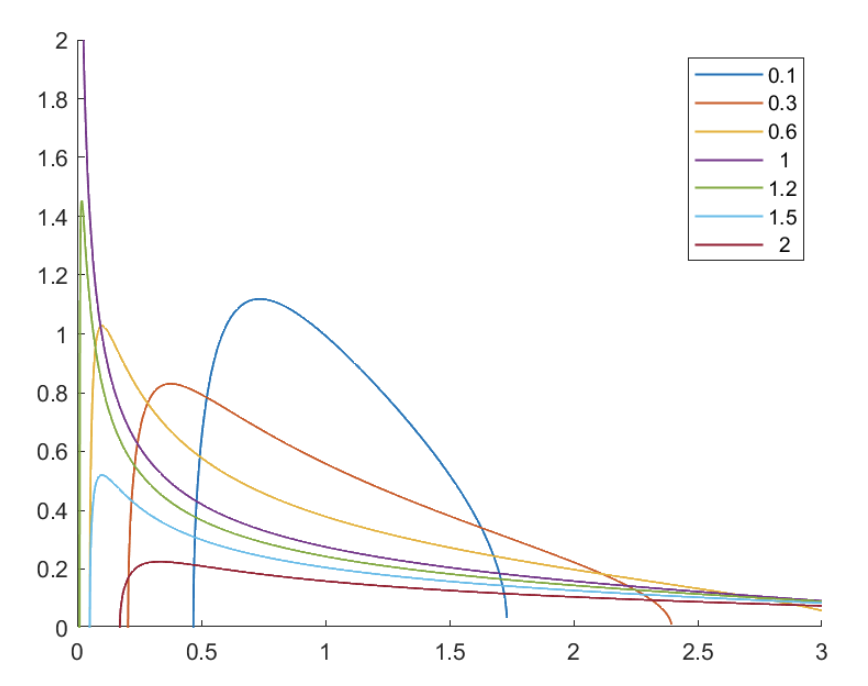
Fig. 10 Illustration when \(\gamma\) goes to zero [Li & Yi 2021]