Contents

Minimum Knapsack

Problem

Input

There are \(n\) kinds of items, each kind of item has a value \(v_i\), integer weight \(w_i\), and infinite number of it.

Objective

Choose a subset of items that maximize value while adhering to knapsack weight constraint \(b\).

Let \(x_i\) be the number of \(i\)-th kind of items in the knapsack, the objective is

\[\begin{split}\begin{aligned} \max &\ \sum _{i=1}^n v_i x_i \\ \text{s.t.} &\ \sum _{i=1}^n w_i x_i \le b,\ x_i \in \mathbb{N} \end{aligned}\end{split}\]

Analysis

Since the objective function and constraint are both linear in \(x_i\), this is a linear programming problem.

Subproblems

The subproblem can be defined by \(k\) and \(y\), where \(k\) is the first \(k \le n\) kinds of items, and \(y\le b\) is the weight constraint. When \(k=n,y=b\) then this is the original problem. The computational order can be \(k=1,\ldots,n\) and for each \(k\), \(y=1,\ldots,b\).

Iterative Relation

Let \(F_{k,y}\) the total optimized value of subproblem \((k,b)\). Consider the last category \(k\). We can either select none, or select one, at each selection step. The iterative relation is

\[\begin{split} F_{k,y} = \max \left\{\begin{array}{ll} F_{k-1,y} & \text { select none } \\ F_{k,y-w_k} + v_k& \text { select one } \end{array}\right\} \end{split}\]

The initialization is

\[\begin{split}\begin{aligned} F_{0,y}&=0, \quad 0\le y \le b \\ F_{k,0}&=0, \quad 0 \le k \le n \\ F_{1,y}&=\left\lfloor\frac{y}{w_{1}}\right\rfloor v_{1} \\ F_{k,y}&=-\infty, \quad y < 0\\ \end{aligned}\end{split}\]

The last line covers the situation when \(y-w_k<0\) in the iterative relation. Since it is not a feasible solution, we assign \(-\infty\) value to it.

Another way of writing the iterative relation is

\[ F_{k,y} = \max _{0 \le x_k \le \left\lfloor\frac{y}{w_{k}}\right\rfloor} \left\{ F_{k-1,y-x_k w_k} + x_k v_k \right\} \]

But to compute \(F_{k,y}\), this way needs \(\left\lfloor\frac{y}{w_{k}}\right\rfloor\) iterations over \(x_k\), which can be \(O(b)\), unlike \(O(1)\) two-value comparison in the previous way.

Algorithm

The DP table can be computed as discussed above. Here we discuss how to trace the solution \(x_i, \ldots, x_n\).

First we define a label function \(i_{k,y}\). Let \(i_{k,y}\) be the maximum label of items added in the solution of subproblem \((k,y)\). We can find that

\[\begin{split} i_{k,y} = \left\{\begin{array}{ll} i_{k-1, y}, & F_{k-1,y} > F_{k,y-w_k} + v_k \\ k, & \text { otherwise } \end{array}\right. \end{split}\]

And the initialization is

\[\begin{split} i_{1,y} = \left\{\begin{array}{ll} 0, & y < w_1 \\ 1, & \text { otherwise } \end{array}\right. \end{split}\]

For instance, for the problem

\[\begin{split} \begin{array}{l} v_{1}=1, \quad v_{2}=3, \quad v_{3}=5, v_{4}=9 \\ w_{1}=2, \quad w_{2}=3, w_{3}=4, w_{4}=7 \\ b=10 \end{array} \end{split}\]

The DP table \(F_{k,y}\) is

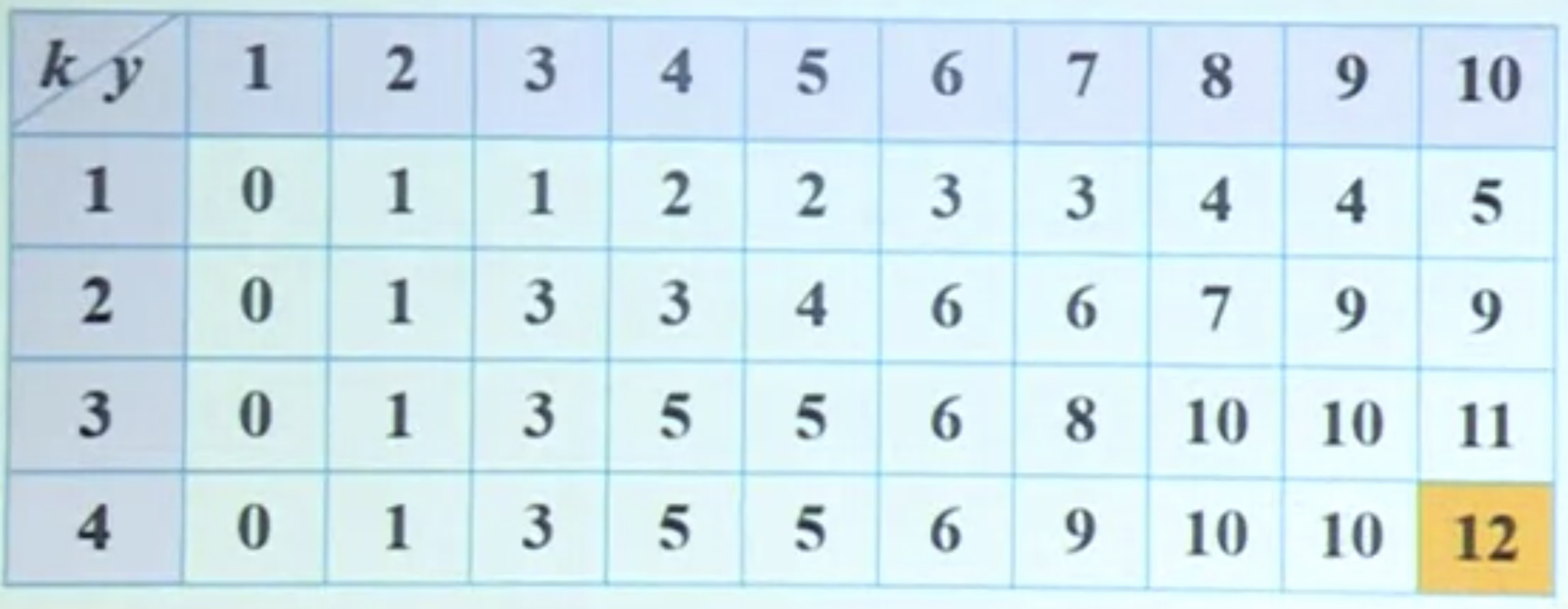
Fig. 33 DP table

and the track table with values \(i_{k,y}\) is

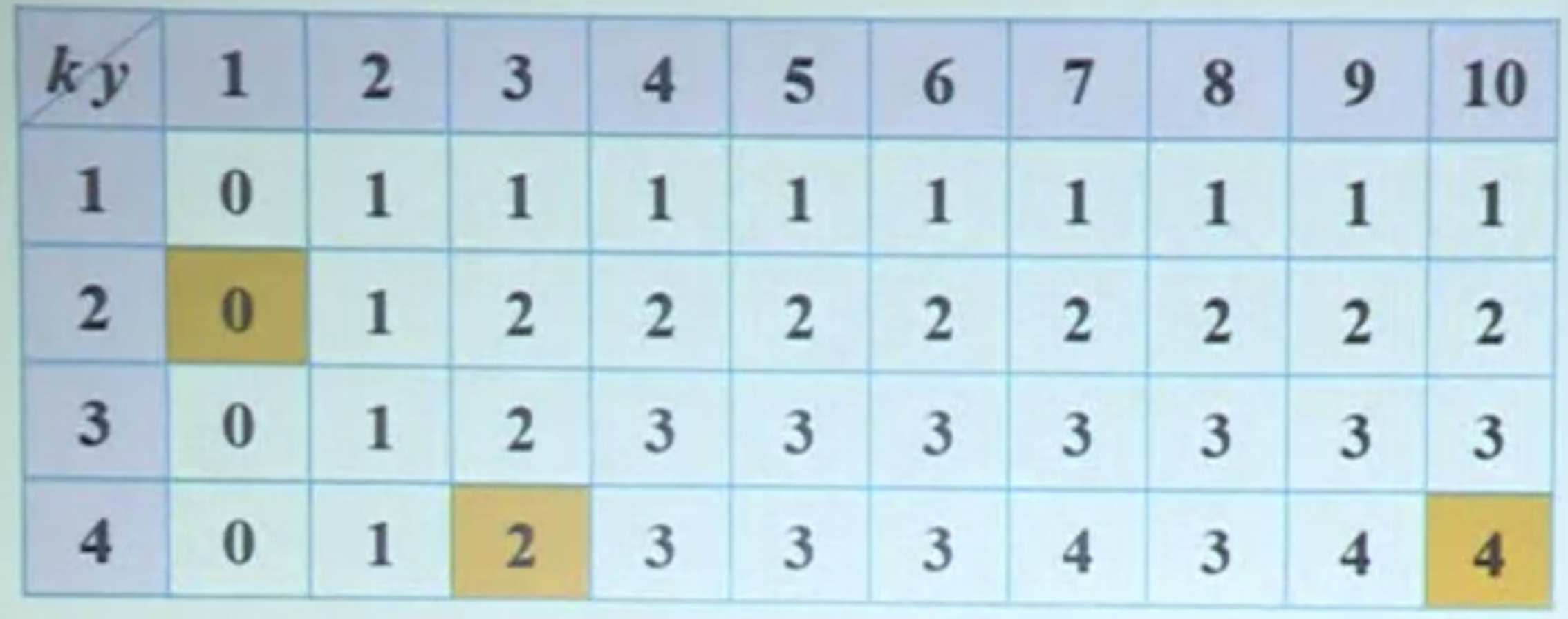
Fig. 34 Track table

To track a solution, we start from the right bottom entry,

  • Since \(i_{4,10} = 4\), this implies \(x_4 \ge 1\). We then go to \(i_{4,10-w_4} = i_{4,3}\), i.e. subproblem \((4,3)\)

  • Since \(i_{4,3}=2\), this implies \(x_3, x_4=0\), and \(x_2 \ge 1\). We then go to \(i_{2,3-w_2} = i_{2,0}\)

  • Since \(i_{2,0}=0\), this implies \(x_2=1, x_1=0\).

Hence, the solution is \(x_1=0, x_2=1, x_3=0, x_4=1\).

The algorithm is

Knapsack: Track Solution

  • input: table \(i_{j,k}\)

  • output: soluiton \(x_1, \ldots, x_k\)

  1. initialize \(x_j\leftarrow 0\) for \(j=1\) to \(n\)

  2. \(y\leftarrow b, j\leftarrow n\) // start from bottom right

  3. \(j \leftarrow i_{j,y}, x_j \leftarrow 1, y\leftarrow y-w_j\) // go to subproblem

  4. while \(i_{j,y} = j\), // add another \(j\)

    1. \(y \leftarrow y-w_j\)

    2. \(x_j \leftarrow x_j + 1\)

  5. If \(i_{j,y}\ne 0\) then goto 3

Complexity

There are \(O(nb)\) entries, and each entry takes \(O(1)\) for the two-value max comparison.

So total \(O(nb)\).

Note that this is pseudo-polynomial time, since \(b\) is not a problem size.

Extensions

Number Constraints

For each kind of item, there is a maximum number to be added.

\[x_i \le n_i\]

One common example is \(n_i=1\), i.e. we can only select none or one for a kind of item.

The iterative relation becomes

\[\begin{split} F_{k,y} = \max \left\{\begin{array}{ll} F_{k-1,y} & \text { select none } \\ F_{\color{red}{k-1},y-w_k} + v_k& \text { select one } \end{array}\right\} \end{split}\]

Multiple Knapsacks

There are multiple knapsack, each has weight constraint \(b_j\).