Huffman Coding¶
Problem¶
- Definition (encoding)
an encoding \(c\) is a mapping from alphabet set \(\Sigma\) to binary string of finite length.
\[ c: \Sigma \rightarrow \cup_{i\ge 1} \left\{ 0, 1 \right\} \]
For instance, the encoding of a word of letters \(w = (\sigma_1, \sigma_2, \ldots, \sigma_n)\) is \(c(w) = c(\sigma_1)c(\sigma_2)\ldots c(\sigma_n)\)
- Definition (unique decoding property)
We say that code \(c\) has unique decoding property iff for every two distinct finite length strings \(s_1 \ne s_2\), we have \(c(s_1) \ne c(s_2)\).
- Definition (prefix code)
A code \(c\) for alphabet \(\Sigma\) is a prefix code iff for all \(\sigma, \sigma ^\prime \in \Sigma\), such that \(\sigma \ne \sigma ^\prime\): \(c(\sigma)\) is not a prefix of \(c(\sigma ^\prime)\)
For instance, the code \(\left\{ a:00, b:0010 \right\}\) is not a prefix code.
- Claim 1
If \(c\) is a prefix code, then it has unique decoding property nd efficient decoding algorithm.
We want to encode as short as possible and be able to decode correctly and efficiently.
For instance, we can use five binary digits to encode \(26\) letters since \(2^5 = 32 > 26\). But this is wasteful since the letter \(x\) appears much less frequently that \(e\). A solution is to use short encoding for frequent letters and long encoding for infrequent letters.
Let the frequency of letter \(a\) in document \(T\) of length \(n\) be
The total code length of the text \(\left\vert c(T) \right\vert\) is
We want to find optimal prefix encoding \(c\) to minimize the average code length
Analysis¶
- Claim 2
There is a one-to-one correspondence between a prefix code and a binary tree. Every leaf corresponds to a letter. Left edge means \(0\) and right edge means \(1\).
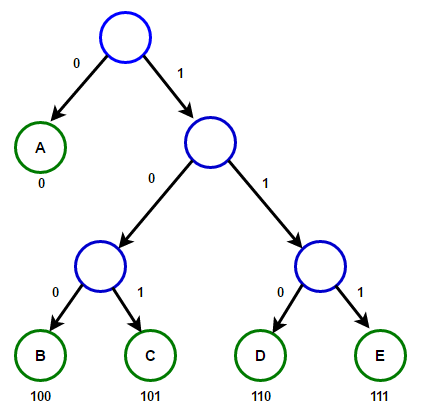
Fig. 32 A binary code tree¶
What is the cost of this binary code tree?
- Properties
code length of a letter \(c(\sigma)\) is the depth of leaf labelled \(c(\sigma)\) in the tree, denoted \(d(\sigma)\).
total cost is \(\mathrm{cost}(T) = \Sigma_{\sigma \in T} f(\sigma) d(\sigma)\)
Now we have converted the code problem to a tree problem to minimize the weighted depth.
- Definition (full binary tree)
A tree is a full binary tree if every non-leaf vertex has exactly 2 children.
- Claim 3
If \(T\) is an optimal tree, it is a full binary tree.
Proof by exchange argument / contradiction
If we delete the non-leaf vertex that has 1 children and move the children up, the resulting tree is still optimal, but we reduce the average depth length, contradiction.
- Claim 4
Suppose there are two letters \(x, y\), with lowest frequency \(f(x) \le f(y) \le f(z)\) for any \(z \ne x, y\). There exists an optimal binary full tree \(T\), where \(x,y\) are siblings, and they lie at the deepest level of the tree.
Proof by exchange argument
Let \(T\) by any optimal tree, \(d\) be the deepest level, \(a\) be any vertex at level \(d\). Let \(b\) be a sibling of \(a\). If \(x\) and \(y\) lie at a shallower level \(d ^\prime < d\) and we switch \((a,b)\) with \((x,y)\), then the average code length of the new tree \(T ^\prime\) does not go up. Consider switch \(a\) and \(x\),
\[\begin{split}\begin{align} \mathrm{cost}(T ^\prime) - \mathrm{cost}(T) &= f(a)[d_{T ^\prime}(a) - d_{T}(a) ] + f(x)[d_{T ^\prime}(x) - d_{T}(x) ] \\ &= f(a)(d ^\prime - d) + f(x)(d - d ^\prime ) \\ &= (d ^\prime - d)[f(a) - f(x)]\\ &\le 0 \\ \end{align}\end{split}\]The proof for the change for switching \(b\) and \(y\) is similar.
- Claim 5
Suppose in a tree \(T\) there are two sibling letters \(x, y\), with frequencies \(f(x), f(y)\) and parent \(z\). Then for the three \(T^{\prime} = T^ \backslash \left\{ x, y \right\} \cup \left\{ z \right\}\), we have
\[\mathrm{cost}(T ) = \mathrm{cost}(T ^\prime) + f(x_1) + f(x_2)\]
The above claims suggest that we can put infrequent letters at the lower levels.
Algorithm¶
Suppose \(\left\vert \Sigma \right\vert > 2\). We use a recursive algorithm \(\mathrm{BuildTree}(\Sigma)\) to build an optimal three \(T\) for alpha bet \(\Sigma\).
When \(\left\vert \Sigma \right\vert = 2\), assign two leaves to the root.
When \(\left\vert \Sigma \right\vert > 2\)
Let \(x, y\) be 2 letters with the smallest frequencies (breaking ties arbitrarily). Consider a new letter \(z\) with frequency \(f(z) = f(x) + f(y)\) and a new alphabet set \(\Sigma ^\prime = \left( \Sigma \backslash \left\{ x,y \right\} \right) \cup \left\{ z \right\}\)
Assign \(T ^\prime \leftarrow \mathrm{BuildTree}(\Sigma ^\prime)\)
Repeat until obtain a final tree \(T\) by adding \(x, y\) as child vertices of \(z\) and deleting the label of \(z\)
Correctness Proof¶
Proof by induction
Induction base: When \(\left\vert \Sigma \right\vert = 2\), the algorithm computes a correct solution.
Induction step: When \(\left\vert \Sigma \right\vert \ge 2\), suppose \(T ^\prime\) is an optimal tree for \(\Sigma ^\prime\), then \(T\) by adding \(x,y\) as siblings lying at the lowest level in \(T ^\prime\) is the optimal solution for \(T = \left( \Sigma \cup \left\{ x,y \right\} \right) \backslash \left\{ z \right\}\).
Proof by contradiction
Suppose there exists an optimal tree \(T^{*} \ne T\) such that \(\mathrm{cost}(T^*) < \mathrm{cost}(T)\), then by Claim 4, \(x, y\) must lie at the lowest level. Consider a new tree \(T^{*\prime} = T^* \backslash \left\{ x, y \right\} \cup \left\{ z \right\}\), then
\[\begin{split}\begin{align} \mathrm{cost}(T^{* ^\prime}) &= \mathrm{cost}(T^*) - f(x) - f(y) \quad \text{by Claim 5}\\ &< \mathrm{cost}(T) - f(x) - f(y) \quad \text{by assumption}\\ &= \mathrm{cost}(T ^\prime) \quad \text{by Claim 5} \end{align}\end{split}\]contradiction to the assumption in the induction step.
Complexity¶
Number of recursive calls: at most \(\left\vert \Sigma \right\vert\)
Time in each call to find the two letters with the smallest frequencies: \(\le \left\vert \Sigma \right\vert\)
Total: \(O(\left\vert \Sigma \right\vert ^2)\)
Review¶
This algorithm code letter by letter. If some words, phrase, or sentences appear frequently, it is better to code them directly.