Contents

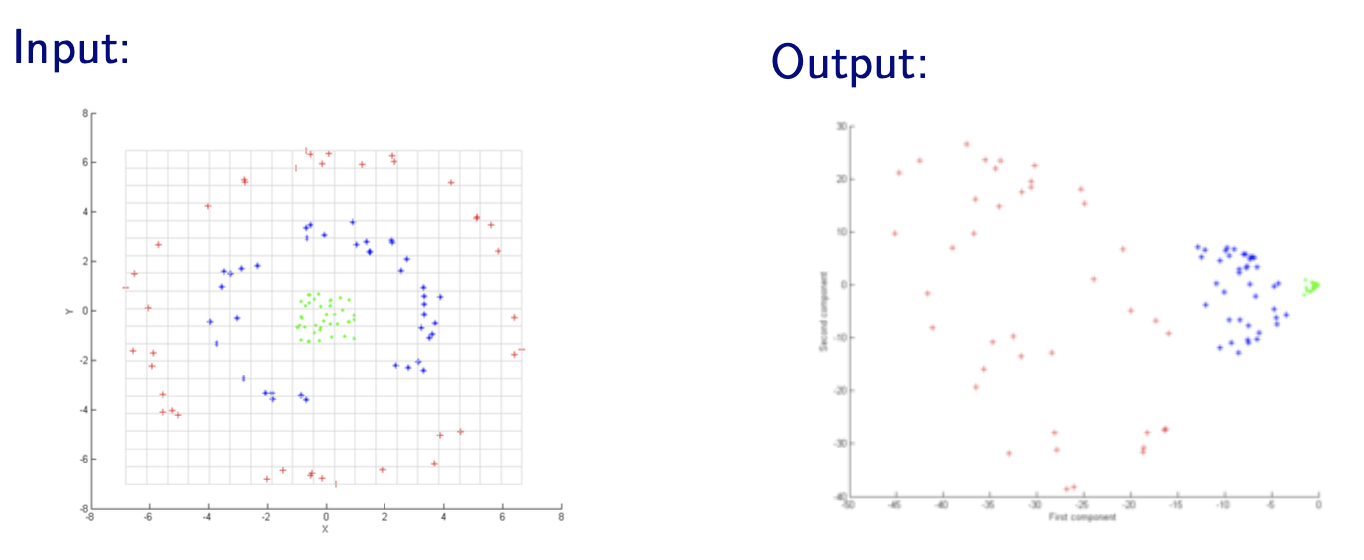
PCA Variants

We introduce three variants of PCA: probabilistic PCA, kernel PCA, and sparse PCA.

Probabilistic PCA

Independently proposed by [Tipping & Bishop 1997, 1999] and [Roweis 1998]

Probabilistic PCA adds a probabilistic component (interpretation) to the PCA model. It provides

  • a way of approximating a Gaussian using fewer parameters (e.g. common noise variance).

  • a way of sampling from the data distribution as a probabilistic model (thus aka sensible PCA).

Objective

In a PPCA model, we first draw low dimensional \(\boldsymbol{z} \in \mathbb{R}^{k}\),

\[ p(\boldsymbol{z}) =\mathcal{N}( \boldsymbol{0}, \boldsymbol{I}) \]

and draw \(\boldsymbol{x} \in \mathbb{R}^{d}, k \leq d\) by

\[ p(\boldsymbol{x} \mid \boldsymbol{z}) =\mathcal{N}\left( \boldsymbol{W} \boldsymbol{z}+\boldsymbol{\mu} , \sigma^{2} \boldsymbol{I}\right) \]

where \(\boldsymbol{W} \in \mathbb{R} ^{d \times k}\)

Or equivalently,

\[ \begin{equation} \boldsymbol{x}=\boldsymbol{W} \boldsymbol{z}+\boldsymbol{\mu} + \boldsymbol{\epsilon} , \text { where } \boldsymbol{\epsilon} \sim \mathcal{N}\left(0, \sigma^{2} \boldsymbol{I}\right) \end{equation} \]

If \(\sigma = 0\) then we get standard PCA.

By the property of multivariate Gaussian, we have

\[ p(\boldsymbol{x})=\mathcal{N}\left(\boldsymbol{\mu} , \boldsymbol{W} \boldsymbol{W}^{\top} +\sigma^{2} \boldsymbol{I}\right) \]

The goal is to estimate the parameter \(\boldsymbol{W} , \boldsymbol{\mu} , \sigma\) that maximize the log likelihood \(\sum_{i=1}^{n} \log p\left(\boldsymbol{x}_{i} \mid \boldsymbol{W} , \boldsymbol{\mu} , \sigma\right)\).

Learning (MLE)

MLE not unique

Before seeking the ML solution, notice that the solution is not unique: if \(\boldsymbol{R}\) is an orthogonal matrix, then \(\widetilde{\boldsymbol{W}} = \boldsymbol{W} \boldsymbol{\boldsymbol{R}}\) is indistinguishable from \(\boldsymbol{W}\)

\[ \widetilde{\boldsymbol{W}} \widetilde{\boldsymbol{W}} ^{\top}=\boldsymbol{W} (\boldsymbol{R} \boldsymbol{R} ^{\top}) \boldsymbol{W} ^{\top} =\boldsymbol{W} \boldsymbol{W} ^{\top} \]

So we will find a solution \(W _{ML}\) up to a rotation \(\boldsymbol{R}\).

Let \(\boldsymbol{C} = \boldsymbol{W} \boldsymbol{W} ^\top + \sigma^2 \boldsymbol{I}_d\). The log likelihood function is

\[ \begin{equation} \sum_{i=1}^{n} \log p\left(\boldsymbol{x}_{i} ; \boldsymbol{W}, \mu, \sigma^{2}\right) = -\frac{n d}{2} \log (2 \pi)-\frac{n}{2} \log |\boldsymbol{C}|-\frac{1}{2} \sum_{i=1}^{n}\left(\boldsymbol{x}_{i}-\boldsymbol{\mu} \right) ^{\top} \boldsymbol{C}^{-1}\left(\boldsymbol{x}_{i}-\boldsymbol{\mu} \right) \end{equation} \]

Setting the derivative w.r.t. \(\boldsymbol{\mu}\) to \(\boldsymbol{0} \) we have

\[\boldsymbol{\mu} _{ML} = \bar{\boldsymbol{x}}\]

i.e. the sample mean. The solution for \(\boldsymbol{W}\) and \(\sigma^2\) is more complicated, but closed form.

\[\begin{split} \begin{equation} \begin{aligned} \boldsymbol{W}_{M L} &=\boldsymbol{U}_{d \times k}\left(\boldsymbol{\Lambda} _{k}-\sigma^{2} \boldsymbol{I}_k\right)^{1 / 2} \boldsymbol{R}_k \\ \sigma_{M L}^{2} &=\frac{1}{d-k} \sum_{j=k+1}^{d} \lambda_{j} \end{aligned} \end{equation} \end{split}\]

EM also works

It is also possible to find the PPCA solution iteratively, visa the EM algorithm. This is useful if doing the eigenvalue decomposition is too computationally demanding.

where

  • \(\boldsymbol{U} _{d \times k}\) is the first \(k\) eigenvectors of the sample covariance matrix \(\boldsymbol{S}\)

  • \(\boldsymbol{\Lambda}_k\) is the diagonal matrix of eigenvalues

  • \(\boldsymbol{R}_k\) is an arbitrary orthogonal matrix

Properties

  • For \(\boldsymbol{R}_k = \boldsymbol{I}_k\) , the solution for \(\boldsymbol{W}\) is just a scaled version (by the diagonal matrix \(\boldsymbol{\Lambda} _k - \sigma^2 \boldsymbol{I} _k\)) of that of standard PCA \(\boldsymbol{U}_{d\times k}\).

  • \(\sigma^2_{ML}\) is the average variance of the discarded dimensions in \(\mathcal{X}\). We view the remaining dimensions as accounting for noise. Their average variance defines the common variance of the noise. The covariance is viewed as

    \[\begin{split} \boldsymbol{\Sigma}=\boldsymbol{U}\left[\begin{array}{cccccccc} \lambda_{1} & \ldots & 0 & \ldots & \ldots & \ldots \\ & \ddots & 0 & \ldots & \ldots & \ldots \\ 0 & \ldots & \lambda_{k} & \ldots & \ldots & \ldots \\ 0 & \ldots & 0 & \sigma^{2} & 0 & \ldots \\ & & & & \ddots & \\ 0 & \ldots & \ldots & \ldots & 0 & \sigma^{2} \end{array}\right] \boldsymbol{U} ^\top \end{split}\]

  • If \(k = d\), i.e., no dimension reduction, then the MLE for the covariance matrix \(\boldsymbol{C}\) of \(\boldsymbol{x}\) is equal to \(\boldsymbol{S}\), which is just the standard ML solution for a Gaussian distribution.

\[ \boldsymbol{C}_{ML} = \boldsymbol{W} _{ML} \boldsymbol{W} _{ML} ^\top + \sigma^2 \boldsymbol{I} = \boldsymbol{U} (\boldsymbol{\Lambda} - \sigma^2 I) \boldsymbol{U} ^\top + \sigma^2 \boldsymbol{I} = \boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{U} ^\top = \boldsymbol{S}. \]

Representation

The conditional distribution of \(\boldsymbol{z}\) given \(\boldsymbol{x}\) is

\[ p(\boldsymbol{z} \mid \boldsymbol{x})=\mathcal{N}\left(\boldsymbol{M}^{-1} \boldsymbol{W} ^{\top} (\boldsymbol{x}- \boldsymbol{\mu} ), \sigma^{2} \boldsymbol{M}^{-1}\right) \]

where \(\boldsymbol{M} = \boldsymbol{W} ^\top \boldsymbol{W} + \sigma^2 \boldsymbol{I}_k\).

A reduced-dimensionality representation of \(\boldsymbol{x}\) is given by the estimated conditional mean

\[ \widehat{\operatorname{E}}\left( \boldsymbol{z} \mid \boldsymbol{x} \right) = \boldsymbol{M} ^{-1} _{ML} \boldsymbol{W} ^\top _{ML}(\boldsymbol{x} - \bar{\boldsymbol{x}}) \]

where \(\boldsymbol{M} _{ML} = \boldsymbol{W} _{ML} ^\top \boldsymbol{W} _{ML} + \sigma^2 _{ML} \boldsymbol{I}_k\).

  • As \(\sigma^2 _{ML} \rightarrow 0\), the posterior mean approaches the standard PCA projection \(\boldsymbol{ z } = \boldsymbol{U} ^\top (\boldsymbol{x} - \bar{\boldsymbol{x} })\)

  • As \(\sigma^2 _{ML}> 0\), the posterior mean “shrinks” the solution in magnitude from standard PCA. Since we are less certain about the representation when the noise is large.

Kernel PCA

Kernel PCA is a nonlinear extension of PCA where dot products are replaced with generalized dot products in feature space computed by a kernel function.

Kernelization

Linear PCA only consider linear subspaces

\[ \boldsymbol{z} = \boldsymbol{W} \boldsymbol{x} \]

To improve this, we can apply feature transformation \(\boldsymbol{\phi}: \mathbb{R} ^d \rightarrow \mathbb{R} ^p\) to include non-linear features, such as \(\boldsymbol{\phi} ([x_1, x_2])= [x_1, x_1^2, x_1 x_2]\).

Then the data matrix changes from \(\boldsymbol{X}_{n \times d}\) to \(\boldsymbol{\Phi}_{n \times p}\). Then we run standard PCA on the new data covariance matrix \(\frac{1}{n} \boldsymbol{\Phi} ^\top \boldsymbol{\Phi}\).

For kernelized problems, the original problem formulation (primal) is in the original feature space \(\mathbb{R} ^d\), and the kernelized problem formulation (dual) is in the transformed space \(\mathbb{R} ^p\).

Note that handcrafting feature transformation \(\boldsymbol{\phi}\) is equivalent to choosing a kernel function \(k(\boldsymbol{x}_1, \boldsymbol{x} _2) = \boldsymbol{\phi}(\boldsymbol{x} _1) ^\top \boldsymbol{\phi}(\boldsymbol{x} _2)\). And there are many advantages choosing kernels instead of handcrafting \(\boldsymbol{\phi}\). After choosing \(k(\cdot, \cdot)\), We can compute the new \(n \times n\) inner product matrix by \(\boldsymbol{K} = \boldsymbol{\Phi} \boldsymbol{\Phi} ^\top\), aka kernel matrix. And the \(k\)-dimensional embeddings for a data vector \(\boldsymbol{x}\) is given by

\[\begin{split} \boldsymbol{z} = \boldsymbol{A} ^\top \left[\begin{array}{c} k(\boldsymbol{x} _1, \boldsymbol{x}) \\ k(\boldsymbol{x} _2, \boldsymbol{x}) \\ \vdots \\ k(\boldsymbol{x} _n, \boldsymbol{x}) \\ \end{array}\right] \end{split}\]

where \(\boldsymbol{A}_{n \times k}\) contains the first \(k\) eigenvectors of the kernel matrix \(\boldsymbol{K}\). That is, the projected data matrix is \(\boldsymbol{Z}_{n \times k} = \boldsymbol{K} \boldsymbol{A}\).

Derivation

Let \(\boldsymbol{C} = \frac{1}{n} \boldsymbol{\Phi} ^\top \boldsymbol{\Phi}\) be the new covariance matrix. To run standard PCA, we solve the eigenproblem

\[ \boldsymbol{C} \boldsymbol{w} = \lambda \boldsymbol{w} \]

Now we show that \(\boldsymbol{w} \in \mathbb{R} ^d\) can be written as a linear combination of the transformed data vectors \(\boldsymbol{\phi} (\boldsymbol{x} _1), \ldots, \boldsymbol{\phi} _1(\boldsymbol{x}_n)\), i.e.,

\[\boldsymbol{w} = \sum_{i=1}^n \alpha_i \boldsymbol{\phi} (\boldsymbol{x}_i ) = \boldsymbol{\Phi} ^\top \boldsymbol{\alpha}\]

To show this, substituting \(\boldsymbol{C} = \boldsymbol{\Phi} ^\top \boldsymbol{\Phi} = \frac{1}{n} \sum_{i=1}^n \boldsymbol{\phi} (\boldsymbol{x}_i ) \boldsymbol{\phi} (\boldsymbol{x}_i )^\top\) to the above equality, we have

\[\begin{split}\begin{aligned} \frac{1}{n} \sum_{i=1}^n \boldsymbol{\phi} (\boldsymbol{x}_i ) \boldsymbol{\phi} (\boldsymbol{x}_i )^\top \boldsymbol{w} &= \lambda \boldsymbol{w} \\ \frac{1}{n\lambda } \sum_{i=1}^n \boldsymbol{\phi} (\boldsymbol{x}_i ) \underbrace{\boldsymbol{\phi} (\boldsymbol{x}_i )^\top \boldsymbol{w}}_{\alpha_i} &= \boldsymbol{w} \\ \end{aligned}\end{split}\]

Then, to find the \(j\)-th eigenvector \(\boldsymbol{w}_j\), it remains to find \(\boldsymbol{\alpha}_j\). Substituting the linear combination back to the eigenproblem gives

\[\begin{split}\begin{aligned} \left( \frac{1}{n} \boldsymbol{\Phi} ^\top \boldsymbol{\Phi} \right)\left( \boldsymbol{\Phi} ^\top \boldsymbol{\alpha} _j \right) &= \lambda_j \boldsymbol{\Phi} ^\top \boldsymbol{\alpha} _j \\ \boldsymbol{\Phi} ^\top \boldsymbol{\Phi} \boldsymbol{\Phi} ^\top \boldsymbol{\alpha} _j &= n\lambda_j \boldsymbol{\Phi} ^\top \boldsymbol{\alpha} _j \\ (\boldsymbol{\Phi} \boldsymbol{\Phi} ^\top ) ^{-1} \boldsymbol{\Phi} \boldsymbol{\Phi} ^\top \boldsymbol{\Phi} \boldsymbol{\Phi} ^\top \boldsymbol{\alpha} _j &= n\lambda_j (\boldsymbol{\Phi} \boldsymbol{\Phi} ^\top ) ^{-1} \boldsymbol{\Phi} \boldsymbol{\Phi} ^\top \boldsymbol{\alpha} _j \quad \text{left multiply } (\boldsymbol{\Phi} \boldsymbol{\Phi} ^\top ) ^{-1} \boldsymbol{\Phi} \\ \boldsymbol{K} \boldsymbol{\alpha} _j &= n \lambda_j \boldsymbol{\alpha} _j\\ \end{aligned}\end{split}\]

Therefore, \(\boldsymbol{\alpha} _j\) is the eigenvector of the kernel matrix \(\boldsymbol{K}\).

To find the embeddings, recall that \(\boldsymbol{w} = \boldsymbol{\Phi} ^\top \boldsymbol{\alpha}\), hence to embed a data vector \(\boldsymbol{x}\),

\[\begin{split}\begin{aligned} \boldsymbol{z} &= \boldsymbol{W} ^\top \boldsymbol{\phi} (x) \\ &= \boldsymbol{A} ^\top \boldsymbol{\Phi} \boldsymbol{\phi} (x) \\ &= \boldsymbol{A} ^\top \left[\begin{array}{c} k(\boldsymbol{x} _1, \boldsymbol{x}) \\ k(\boldsymbol{x} _2, \boldsymbol{x}) \\ \vdots \\ k(\boldsymbol{x} _n, \boldsymbol{x}) \\ \end{array}\right]\\ \end{aligned}\end{split}\]

In fact, we don’t need the exact form of \(\boldsymbol{\phi}\) at all.

Mean normalization of \(\boldsymbol{K}\)

We’ve implicitly assumed zero-mean in the new feature space \(\mathbb{R} ^p\), but it is usually not. Hence, we should modify \(\boldsymbol{K}\) by

\[ \boldsymbol{K} ^c = \boldsymbol{C} \boldsymbol{K} \boldsymbol{C} \]

where \(\boldsymbol{C} = \left(\boldsymbol{I}-\frac{1}{n} \boldsymbol{1} \boldsymbol{1}^{\top}\right)\) is the centering matrix. Then we solve for the eigenvectors of \(\boldsymbol{K} ^c\)

Learning

From the analysis above, the steps to train a kernel PCA are

  1. Choose a kernel function \(k(\cdot, \cdot)\).

  2. Compute the centered kernel matrix \(\boldsymbol{K} ^c = (\boldsymbol{I} - \boldsymbol{u} \boldsymbol{u} ^\top )\boldsymbol{K}(\boldsymbol{I} - \boldsymbol{u} \boldsymbol{u} ^\top)\)

  3. Find the first \(k\) eigenvectors of \(\boldsymbol{K} ^c\), stored as \(\boldsymbol{A}\).

Then

  • to project a new data vector \(\boldsymbol{x}\),

    \[\begin{split}\begin{aligned} \boldsymbol{z} &= \boldsymbol{A} ^\top \left[\begin{array}{c} k(\boldsymbol{x} _1, \boldsymbol{x}) \\ k(\boldsymbol{x} _2, \boldsymbol{x}) \\ \vdots \\ k(\boldsymbol{x} _n, \boldsymbol{x}) \\ \end{array}\right]\\ \end{aligned}\end{split}\]

  • to project the training data,

    \[\boldsymbol{Z} ^\top = \boldsymbol{A} ^\top \boldsymbol{K} \text{ or } \boldsymbol{Z} = \boldsymbol{K} \boldsymbol{A} \]

  • to project a new data matrix \(\boldsymbol{Y} _{m \times d}\),

    \[\begin{split} \boldsymbol{Z} _y ^\top = \boldsymbol{A} ^\top \left[\begin{array}{ccc} k(\boldsymbol{x} _1, \boldsymbol{y_1}) & \ldots &k(\boldsymbol{x} _1, \boldsymbol{y_m}) \\ k(\boldsymbol{x} _2, \boldsymbol{y_1}) & \ldots &k(\boldsymbol{x} _2, \boldsymbol{y_m}) \\ \vdots &&\vdots \\ k(\boldsymbol{x} _n, \boldsymbol{y_1}) & \ldots &k(\boldsymbol{x} _n, \boldsymbol{y_m}) \\ \end{array}\right]\\ \end{split}\]

Choice of Kernel

As discussed, in practice, we don’t engineer \(\boldsymbol{\phi}(\cdot)\), but directly think about \(k(\cdot, \cdot)\).

  • One common choice of kernel is radial basis function (RBF), aka Gaussian kernel

    \[ k\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{2}\right)=e^{\frac{\left\| \boldsymbol{x}_{1}-\boldsymbol{x}_{2} \right\| ^{2}}{2 \sigma^{2}}} \]

    where the standard deviation (radius) \(\sigma\) is a tuning parameter. Note that RBF corresponds to an implicit feature space \(\mathbb{R} ^p\) of infinite dimensionality \(p\rightarrow \infty\).

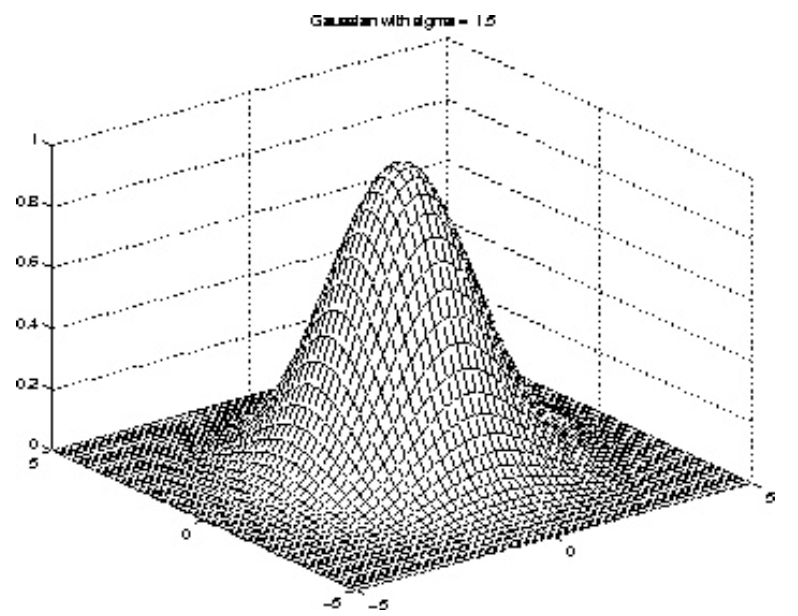
Fig. 97 Gaussian kernels

  • Polynomial kernel

    \[ k\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{2}\right)=\left(1+\boldsymbol{x}_{1}^{\top} \boldsymbol{x}_{2}\right)^{p} \]

    where the polynomial degree \(p\) is a tuning parameter. \(p=2\) is common.

Pros and Cos

Pros

  • Kernel PCA can do out-of-sample projection, PCA cannot

  • Kernel PCA works well when

    • the data is non-linear and fit the chosen kernel.

      Fig. 98 Kernel PCA with a RBF kernel on points [Livescu 2021].

    • there is much noise in the data

      Fig. 99 Kernel PCA on images [Livescu 2021].

Cons

  • Kernel PCA works bad when the data lies a special manifold

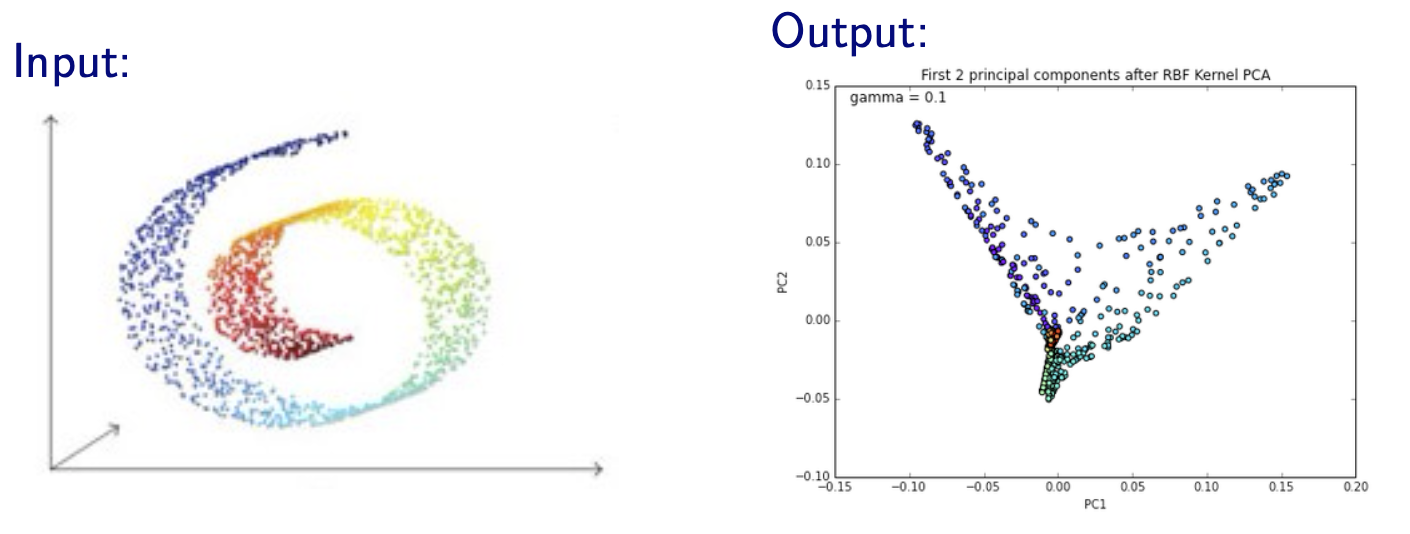
    Fig. 100 Kernel PCA with RBF kernel on a Swiss roll manifold [Livescu 2021]

  • Computationally expensive to compute the \(n \times n\) pairwise kernel values in \(\boldsymbol{K}\) when \(n\) is large. Remedies include

    • use subset of the entire data set

    • use kernel approximation techniques

      • approximate \(\boldsymbol{K} \approx \boldsymbol{F}^\top \boldsymbol{F}\) where \(\boldsymbol{F} \in \mathbb{R} ^{m \times n}, k \ll m \ll n\). The value of \(m\) should be as large as you can handle.

      • for RBF kernels, there is one remarkable good approximation (due to Fourier transform properties) called random Fourier features (Rahimi & Recht 2008), which replaces each data point \(\boldsymbol{x}_i\) with

        \[ \left[\cos \left(\boldsymbol{w}_{1}^{\top} \boldsymbol{x}_{i}+b_{1}\right) \ldots \cos \left(\boldsymbol{w}_{m}^{\top} \boldsymbol{x}_{i}+b_{m}\right)\right]^{\top}=\boldsymbol{f} _{i} \]

        where

        \[\begin{split} \begin{aligned} b_{1}, \ldots, b_{m} & \sim \operatorname{Unif}[0,2 \pi] \\ \boldsymbol{w}_{1}, \ldots, \boldsymbol{w}_{m} & \sim \mathcal{N}\left(0, \frac{2}{\sigma^{2}} \boldsymbol{I}_d \right) \end{aligned} \end{split}\]

    • just don’t use kernel methods if computation is an issue

Relation to

Standard PCA

Clearly, kernel PCA with linear kernel \(k(\boldsymbol{x} , \boldsymbol{y} ) = \boldsymbol{x} ^\top \boldsymbol{y}\) is equivalent to a standard PCA. That is, they give the same projection.

Derivation

From the analysis above we know that the kernel PCA with linear kernel gives projection of \(\boldsymbol{x}\) as

\[\boldsymbol{z} = \boldsymbol{A} ^\top \boldsymbol{X} \boldsymbol{x}\]

where \(\boldsymbol{A}_{n \times k}\) is the matrix that stores \(\alpha_{ij}\). Then it remains to prove that \(\boldsymbol{A} ^\top \boldsymbol{X} = \boldsymbol{U} ^\top\) where \(\boldsymbol{U}\) is the projection matrix in conventional PCA: \(\boldsymbol{z} = \boldsymbol{U} ^\top \boldsymbol{x}\). where \(\boldsymbol{A}_{n \times k}\) is the matrix that stores \(\alpha_{ij}\).

Note that in kernel PCA, \(\boldsymbol{\alpha}_j\) are the eigenvectors of the kernel matrix \(\boldsymbol{K}\) since

\[ \boldsymbol{K} \boldsymbol{\alpha} _j = n \lambda_j \boldsymbol{\alpha} _j \]

If we use linear kernel, then \(\boldsymbol{K} = \boldsymbol{X} \boldsymbol{X} ^\top\) and the above relation becomes

\[ \boldsymbol{X} \boldsymbol{X} ^\top \boldsymbol{\alpha} _j = n \lambda_j \boldsymbol{\alpha} _j \]

Hence, the matrix \(\boldsymbol{A}\) contains the first \(k\) eigenvectors of the Gram matrix \(\boldsymbol{X} \boldsymbol{X} ^\top\).

Now we consider conventional PCA. The projection in \(\mathbb{R} ^k\) is given by

\[ \boldsymbol{z} = \boldsymbol{U} ^\top \boldsymbol{x} \]

where \(\boldsymbol{U} _{n \times k}\) contains the first \(k\) eigenvectors of the matrix \(\boldsymbol{X} ^\top \boldsymbol{X}\).

Let the singular value decomposition of \(\boldsymbol{X}\) be

\[ \boldsymbol{X} = \boldsymbol{A} \boldsymbol{\Sigma} \boldsymbol{U} ^\top \]

  • The EAD of \(\boldsymbol{X} ^\top \boldsymbol{X}\) is

    \[\boldsymbol{X} ^\top \boldsymbol{X} = \boldsymbol{U} \boldsymbol{\Sigma} ^\top \boldsymbol{\Sigma} \boldsymbol{U} = \boldsymbol{U} \boldsymbol{D} \boldsymbol{U}\]

    where the diagonal entries in \(\boldsymbol{D}\) are the squared singular values \(\sigma^2 _j\) for \(j=1,\ldots, d\).

  • The EAD for the Gram matrix \(\boldsymbol{G}\)

    \[ \boldsymbol{G}_{n \times n}=\boldsymbol{X} \boldsymbol{X}^{\top}=\boldsymbol{A} \boldsymbol{\Sigma} \boldsymbol{\Sigma}^{\top} \boldsymbol{A}^{\top}=\boldsymbol{A} \boldsymbol{\Lambda} \boldsymbol{A}^{\top}=\boldsymbol{A}_{[: d]} \boldsymbol{D} \boldsymbol{A}_{[: d]}^{\top} \]

    where

    \[\begin{split} \boldsymbol{\Lambda}_{n \times n}=\left[\begin{array}{cc} \boldsymbol{D}_{d \times d} & \mathbf{0} \\ \mathbf{0} & \mathbf{0}_{(n-d) \times(n-d)} \end{array}\right] \end{split}\]

Let \(\boldsymbol{a} _j\) be an eigenvector of \(\boldsymbol{G}\) with eigenvalue \(\sigma^2 _j\). Pre-multiplying \(\boldsymbol{G} \boldsymbol{a}_j = \sigma^2 _j \boldsymbol{a} _j\) by \(\boldsymbol{X} ^\top\) yields

\[\begin{split}\begin{aligned} \boldsymbol{X} ^\top (\boldsymbol{X} \boldsymbol{X} ^\top) \boldsymbol{a} _j &= \boldsymbol{X} ^\top (\sigma^2 _j \boldsymbol{a} _j) \\ \Rightarrow \qquad \boldsymbol{X} ^\top \boldsymbol{X} (\boldsymbol{X} ^\top \boldsymbol{a} _j) &= \sigma^2 _j (\boldsymbol{X} ^\top \boldsymbol{a} _j) \end{aligned}\end{split}\]

Hence, we found that \(\boldsymbol{X} ^\top \boldsymbol{a} _j\) is an eigenvector of \(\boldsymbol{X} ^\top \boldsymbol{X}\) with eigenvalue \(\sigma^2 _j\), denoted \(\boldsymbol{u} _j\),

\[ \boldsymbol{u} _j = \boldsymbol{X} ^\top \boldsymbol{a} _j \]

That is, there is a one-one correspondence between the first \(d\) eigenvectors of \(\boldsymbol{G}\) and those of \(\boldsymbol{X} ^\top \boldsymbol{X}\). More specifically, we have,

\[ \boldsymbol{U} _{[:d]} = \boldsymbol{X} ^\top \boldsymbol{A} _{[:d]} \]

which completes the proof.

\(\square\)

Graph-based Spectral Methods

Both are motivates as extensions of MDS and involves a \(n \times n\) matrix.

We can view kernel in kernel PCA as the edge weights in graph-based spectral methods. But the main difference is that in kernel PCA we compute the kernel value of every pair of data points (computationally demanding), but in graph-based spectral methods we only compute weights between points that are neighbors, charactrized by an integer \(k\) or distance \(\epsilon\).

Neural Networks

Kernel PCA can be viewed as a neural network of one single layer with certain constraints.

Let

  • \(k(\boldsymbol{x}, \boldsymbol{w} )\) be a kernel node parameterized by \(\boldsymbol{w}\) and output the kernel value.

  • \(w_{ij}\) be the weight of the edge from the \(i\)-th input node to the \(j\)-th hidden node

  • \(v_{ij}\) be the weight of the edge from the \(i\)-th hidden node to the \(j\)-th output node

Recall our objective is to find \(\boldsymbol{\alpha}_1, \boldsymbol{\alpha} _2, \ldots\) such that the \(j\)-th entry in the embedding is

\[\begin{split} z_j=\boldsymbol{\alpha}_j^{\top}\left[\begin{array}{c} k\left(\boldsymbol{x}_{1}, \boldsymbol{x}\right) \\ k\left(\boldsymbol{x}_{2}, \boldsymbol{x}\right) \\ \vdots \\ k\left(\boldsymbol{x}_{n}, \boldsymbol{x}\right) \end{array}\right] \end{split}\]

So the neural network can be designed as

  • Input layer:

    • \(d\) nodes, which represent \(\boldsymbol{x} \in \mathbb{R} ^d\)

  • Kernel layer:

    • \(n\) kernel nodes, where the \(j\)-th node represents \(k(\boldsymbol{x}, \boldsymbol{x}_i)\)

    • Fixed weights where \(w_{ij}=1\)

    • The activation function is simply the identity function

  • Hidden layer

    • \(k\) nodes, which represent \(\boldsymbol{z} \in \mathbb{R} ^k\)

    • Weights \(v_{ij} = \alpha_{ij}\)

    • The activation function is simply the identity function

  • Output layer

    • \(n\) nodes, which represents reconstruction of kernel layer (similar to PCA as autoencoders)

    • Weights \(\alpha_{ji}\)

    • The activation function is simply the identity function

    • Loss: reconstruction loss

In short, we transform the input from \(n\times d\) data matrix \(\boldsymbol{X}\) to \(n\times n\) kernel matrix \(\boldsymbol{K}\), and run PCA. In this way, the learned weights \(\boldsymbol{A}\) are the eigenvectors of \(\boldsymbol{K} ^{\top} \boldsymbol{K}\) (analogous to \(\boldsymbol{X} ^{\top} \boldsymbol{X}\) in PCA), which are the same as \(\boldsymbol{K}\), i.e. what we want for.

Sparse PCA

Recall that \(Z\) is a linear combination of the variables \(X_j\). The original optimization problem is

\[ \max\ \boldsymbol{a} ^{\top} \boldsymbol{S} \boldsymbol{a} \quad \text{s.t. } \|\boldsymbol{a} \|_2=1 \]

If we want to impose the number of non-zero coefficient \(a_i\), we can add constraint \(\left\| \boldsymbol{a} \right\| _0 \le k\).

Hui ZOU, Trevor HASTIE, and Robert TIBSHIRANI, 2006

Eigen-space Approach

The problem can be formulated as

\[ \max\ \boldsymbol{\beta} ^{\top} \boldsymbol{S} \boldsymbol{\beta} \quad \text{s.t. } \|\boldsymbol{\beta}\|_2=1, \left\| \boldsymbol{\beta} \right\| _0 \le k \]

Often \(k \ll p\) is desired when \(p\) is large.

Similar to sequential approach in PCA, after obtaining the first principal component \(\boldsymbol{\beta} _1\), we define

\[ \boldsymbol{S} _1 = \boldsymbol{S} - (\boldsymbol{\beta} ^{\top}_1 \boldsymbol{S} \boldsymbol{\beta}_1) \boldsymbol{\beta}_1 \boldsymbol{\beta} ^{\top} _1 \]

and the second sparse principal components can be found by solving the problem

\[ \max\ \boldsymbol{\beta} ^{\top} \boldsymbol{S}_1 \boldsymbol{\beta} \quad \text{s.t. } \|\boldsymbol{\beta}\|_2=1, \left\| \boldsymbol{\beta} \right\| _0 \le k \]

However, unlike the original principal components \(\boldsymbol{a} _i\)’s, the \(\boldsymbol{\beta} _i\)’s are not necessarily orthogonal or uncorrelated to each other without imposing further conditions. In addition, solving this optimization problem turns out to be a very computationally demanding process.

Penalized Regression Approach

One of the alternative approaches for sparse PCA is to devise PCA in a regression setting, then utilize the shrinkage method in linear regression.

Consider the \(i\)-th principal direction \(\boldsymbol{v}_i\) and the corresponding score \(\boldsymbol{z}_i = \boldsymbol{X} \boldsymbol{v}_i\). Now we want a sparse principal direction \(\boldsymbol{\beta}\), but keep the new score \(\boldsymbol{X} \boldsymbol{\beta}\) as close to \(\boldsymbol{z}_i\) as possible. The problem can be formulated as a penalized regression

\[ \min_{\boldsymbol{\beta}}\ \left\| \boldsymbol{z}_i - \boldsymbol{X} \boldsymbol{\beta} \right\|^2 + \lambda \left\| \boldsymbol{\beta} \right\| \]

If we use Ridge regression, then it can be shown that the sparse optimizer \(\boldsymbol{\beta}_{\text{ridge} }\) is parallel to the principal direction \(\boldsymbol{v}_i\):

\[ \frac{\hat{\boldsymbol{\beta}} _{\text{ridge} }}{\left\| \hat{\boldsymbol{\beta}} _{\text{ridge} } \right\| } = \boldsymbol{v}_i \]

Derivation

Consider SVD \(\boldsymbol{X} = \boldsymbol{U} \boldsymbol{D} \boldsymbol{V} ^{\top}\), then \(\boldsymbol{X} ^{\top} \boldsymbol{X} = \boldsymbol{V} \boldsymbol{D} ^2 \boldsymbol{V} ^{\top}\),

\[\begin{split} \begin{aligned} \hat{\boldsymbol{\beta}}_{\text {ridge }} &=\left(\boldsymbol{V} \boldsymbol{D} ^{2} \boldsymbol{V} ^{\prime}+\lambda \boldsymbol{I} \right)^{-1} \boldsymbol{X} ^{\prime} \boldsymbol{z}_i \\ &=\left[\boldsymbol{V} \left(\boldsymbol{D} ^{2}+\lambda \boldsymbol{I}\right) \boldsymbol{V}^{\prime}\right]^{-1} \boldsymbol{X} ^{\top} \boldsymbol{X} \boldsymbol{v}_i \\ &=\boldsymbol{V}^{\prime-1}\left(\boldsymbol{D}^{2}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{V}^{-1} \boldsymbol{V} \boldsymbol{D}^{2} \boldsymbol{V}^{\prime} \boldsymbol{v}_i \\ &=\boldsymbol{V}\left(\boldsymbol{D}^{2}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{D}^{2} \boldsymbol{e}_{i} \\ &=\boldsymbol{V} \frac{d_{i i}^{2}}{d_{i i}^{2}+\lambda} \boldsymbol{e}_{i} \\ &=\frac{d_{i i}^{2}}{d_{i i}^{2}+\lambda} \boldsymbol{\boldsymbol{v}}_{i} \end{aligned} \end{split}\]

Hence the loadings are scaled down (attenuated), but still non-zero. We can continue to add \(L_1\) norm. The problem becomes

\[ \min_{\boldsymbol{\beta}}\ \left\| \boldsymbol{z}_i - \boldsymbol{X} \boldsymbol{\beta} \right\|^2 + \lambda_1 \left\| \boldsymbol{\beta} \right\|_1 + \lambda_2 \left\| \boldsymbol{\beta} \right\|_2 ^2 \]

A larger \(\lambda_1\) will give fewer non-zero component of \(\hat{\boldsymbol{\beta}}\). The estimated coefficients would be an approximation of the principal direction \(\boldsymbol{v} _i\)

\[ \frac{\hat{\boldsymbol{\beta} }}{\left\| \hat{\boldsymbol{\beta} } \right\| } \approx \boldsymbol{v} _i \]

where only a few components in \(\hat{\boldsymbol{\beta}}\) is non-zero.

Implementation in R with function spca

In R function spca in library elasticnet, there are many options

  • type=

    • predictor: use data matrix as input

    • Gram: use covariance matrix or correlation matrix as input

  • sparse='varnum', para=c(nnz_1, nnz_2): To find sparse loadings, use number of non-zero entries as criteria \(\left\| \boldsymbol{\beta}_i\right\|_0 \le \texttt{nnz_i}\). The numbers are specified in para.

  • sparse='penalty', para=c(norm_1, norm_2): To find sparse loadings, use the 1-norm of loadings as criteria \(\left\| \boldsymbol{\beta}_i\right\|_1 \le \texttt{norm_i}\). The values of norms are specified in para.