Contents

Topic Models

Topic models are generative “mixture” models for documents.

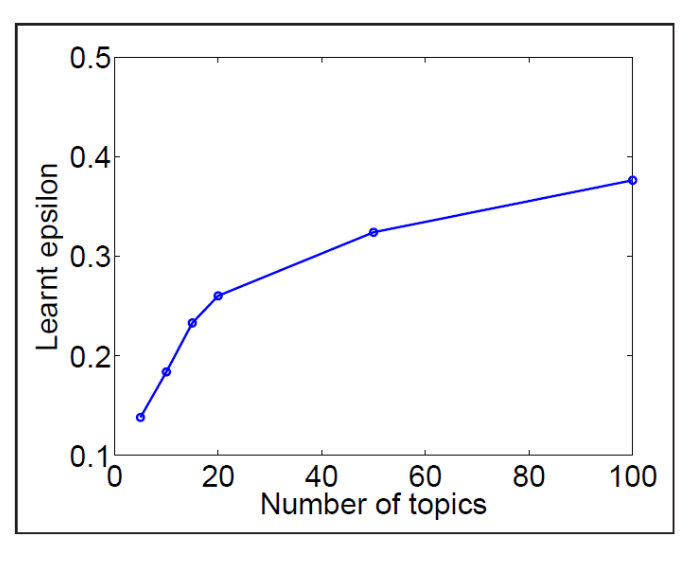
The data we have in hand are \(D\) documents. Each document \(d\) has \(n_d\) words. Topic model assumes that there is a topic \(t_d\) for each document, which is latent, unobservable.

Generative Process

Now we generate the \(D\) documents.

Assumptions

For a document \(d\),

  • Its topics \(t_d\) is unknown. Suppose there are \(k_t\) kinds of possible topics, then \(t_d\) can be drawn from a multinomial distribution parameterized by \(\boldsymbol{\alpha} \in \mathbb{R} ^{k_t}\).

    \[t_d \sim \operatorname{Multinomial}(\boldsymbol{\alpha}) \]

  • The words \(w_1, \ldots, w_{n_d}\) are i.i.d. drawn from multinomial distribution of \(k_w\) kinds of words, parameterized by \(\boldsymbol{\beta} \in \mathbb{R} ^{k_w}\). The words distribution can be determined by the document topic \(t_d\), i.e. \(\boldsymbol{\beta} _{t_d}\), hence

    \[w \sim \operatorname{Multinomial}(\boldsymbol{\beta}_{t_d})\]

  • We can impose prior distributions on \(\boldsymbol{\beta}\) and \(\boldsymbol{\alpha}\), which are Dirichlet distributions, parameterized by \(\boldsymbol{\eta}\) and \(\boldsymbol{\theta}\) respectively.

    \[\begin{split}\begin{aligned} \boldsymbol{\beta} &\sim \operatorname{Dirichlet}(\boldsymbol{\eta} ) \\ \boldsymbol{\alpha} &\sim \operatorname{Dirichlet}(\boldsymbol{\theta} ) \end{aligned}\end{split}\]

Hence, to generate \(D\) documents, each with \(\sum_{d=1}^D n_d\) number of random words, the steps are

  • For each document \(d=1, \ldots, D\)

    • Draw a topic vector \(\boldsymbol{\alpha} \sim \operatorname{Dirichlet}(\boldsymbol{\theta})\)

    • Draw \(k_t\) vectors \(\boldsymbol{\beta}, \ldots, \boldsymbol{\beta}_{k_t} \sim \operatorname{Dirichlet}(\boldsymbol{\eta})\)

    • Generate words: for \(1, \ldots, n_d\)

      • Draw a topic \(t\sim \operatorname{Multinomial}(\boldsymbol{\alpha} )\)

      • Draw a word \(w\sim \operatorname{Multinomial}(\boldsymbol{\beta}_{t})\)

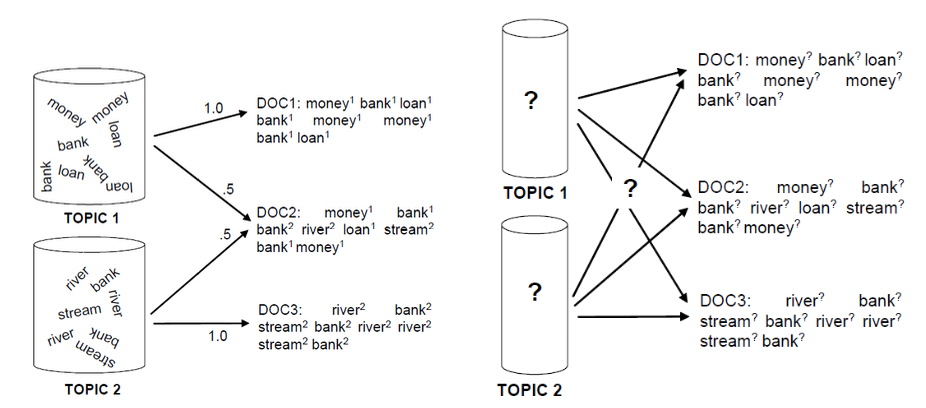
Fig. 142 Topic model (generation vs estimation)

Estimation

In a document of words \(w_1, \ldots, w_{n_d}\), we want to estimate the underlying word distribution \(\boldsymbol{\beta} = \left[ \beta_1, \ldots, \beta_{k_w} \right]\). A simple approach is to use maximum likelihood

\[\widehat{\boldsymbol{\beta}}=\underset{\boldsymbol{\beta}}{\operatorname{argmax}} p\left(w_{1}, \ldots, w_{n_d} ; \boldsymbol{\beta}\right)\]

For some word labeled \(m\), this is

\[ \widehat{\beta}_m = \frac{\#\left(w_{i}= m\right)}{N} \]

Other variables include \(t\)’s, \(\boldsymbol{\alpha}\)’s, which can be estimated by Expectation Maximization (EM) algorithm and sampling-based methods (MCMC and Gibbs sampling)

The learned results are like

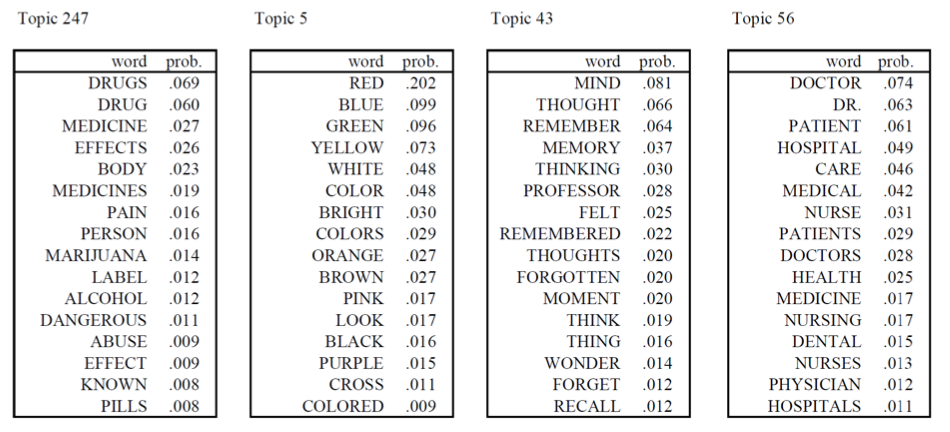
Fig. 143 Learned words distribution parameters \(\boldsymbol{\beta} _t\) by topics [Steyvers & Griffiths, 2007]

Hidden Topic Markov Models

Recall that in topic models, we do not consider the dependency of topics between a sequence of words.

Hidden topic Markov model improve this. It view the topic behind a word as a hidden state. Let \(\epsilon\) be the probability of ending sentence and drawing a new topic. Clearly, as \(\epsilon\) increases, we switch topic mode frequently, and the number of topics should increases.

Fig. 144 How \(\epsilon\) affect number of topics in a sentence.

HTMM can decrease perplexity too.

Fig. 145 HTMM decreases perplexity as number of topics increases

Example

Consider two paragraphs. If we use topic mixture model (smoother LDA), the topics seems random. For the word “support”, all appearances are all from the same topic.

Fig. 146 Topic mixture model (smoothed LDA) results, colors are topic labels [Livescu 2021]

Using HTMM, the results are much better. It distinguish “support” from support vector and support in research.

Fig. 147 HTMM results, colors are topic labels [Livescu 2021]