Machine Learning Basics¶
Structure¶
For each model, we introduce
Objective
What is the structural form of the model
What quantity to optimize
Learning
Aka training, fitting, estimation
How to train a model capable for prediction
Properties
Properties of the model
Model Selection
How to select a good hyperparameter
Interpretation
The logic behind the model
The parameter of the model
The results of the model
Extension
Variants of the model
Proximity Measures¶
There are many similarity or dissimilarity measures (jointly called proximity measures) used in machine learning, all with certain degrees of subjectivity. Several important aspects should be considered.
The nature of the variables,
The scales of measurement,
Subject matter knowledge.
Some commonly used distance measures for two vectors \(\boldsymbol{x} , \boldsymbol{y} \in \mathbb{R} ^{p}\)
Euclidean distance \(d(\boldsymbol{x}, \boldsymbol{y})=\sqrt{(\boldsymbol{x}-\boldsymbol{y})^{\prime}(\boldsymbol{x}-\boldsymbol{y})}\)
Statistical or Mahalanobis distance \(d(\boldsymbol{x}, \boldsymbol{y})=\sqrt{(\boldsymbol{x}-\boldsymbol{y})^{\prime} \boldsymbol{S} ^{-1}(\boldsymbol{x}-\boldsymbol{y})}\), \(\boldsymbol{S}\) the sample covariance matrix
Minkowski metric: \(d(\boldsymbol{x}, \boldsymbol{y})=\left(\sum_{i=1}^{p}\left|\boldsymbol{x}_{i}-y_{i}\right|^{m}\right)^{1 / m}\). Important cases in application: \(m=1,2, \infty\).
Canberra metric: \(d(\boldsymbol{x}, \boldsymbol{y})=\sum_{i=1}^{p} \frac{\left|\boldsymbol{x}_{i}-y_{i}\right|}{\left|\boldsymbol{x}_{i}\right|+\left|y_{i}\right|}\), aka normalized Manhattan distance (city block or taxicab distance)
Czekanowski coefficient \(d(\boldsymbol{\boldsymbol{x}}, \boldsymbol{y})=1-\frac{2 \sum_{i=1}^{p} \min \left(\boldsymbol{x}_{i}, y_{i}\right)}{\sum_{i=1}^{P}\left(\boldsymbol{x}_{i}+y_{i}\right)}\)
For two sets \(A, B\)
Jaccard similarity: uses size of intersection/union \(=\frac{|A \cap B|}{|A \cup B|}\)
Simpson overlap coefficient: \(\frac{|A \cap B|}{\min \{|A|,|B|\}}\)
Sorensen-Dice coefficient: \(\frac{2|A \cap B|}{|A|+|B|}\)
Applications¶
Vision¶
Tasks
Classification
assign a label to an object in the image, e.g. digit, object …
error measure: top-5 error
sometimes labeling is very expensive, e.g. medical images
Detection
find a tight bounding box on the (visible portion) of each object from a given class
error measure: accuracy of the bounding box, e.g., overlap with true box
note: multiple classes per image, multiple instances per class
Segmentation
find pixel-level outline of each object (more precise than a box)
instance level: separate instances of objects
category level (semantic segmentation): label pixels with class, do not distinguish between instances.
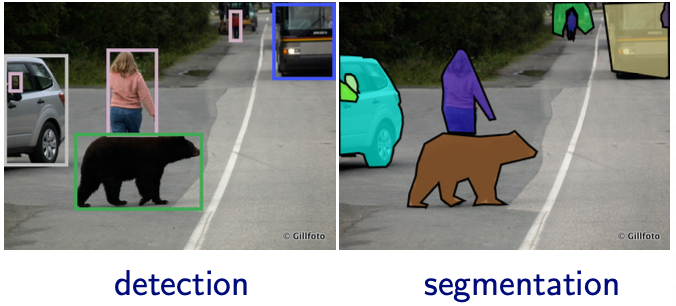
Fig. 38 Image detection and segmentation [Shakhnarovich 2021]¶
For other tasks, usually use transfer learning
Train a NN on ImageNet for classification
For a new task,
if small data set, retrain only the classifier (treat CNN as fixed feature extractor)
if medium data set, finetune higher layers or even retrain all of the network
Speech¶
Speech processing = getting machines to do everything humans do when listening to/producing/learning speech
Listening (speech as input)
Who is speaking? (Speaker identification)
What are the speaker characteristics (gender, age, dialect, …)?
Separating speech from background audio, other speakers (Speech separation)
What is the speaker’s emotional/health state? (Emotion recognition, …)
What words is the speaker uttering? (Speech recognition)
Was a particular word/phrase uttered? (Keyword spotting/spoken term detection)
What is the semantic information conveyed? (Spoken language understanding)
Other “NLP” tasks on speech (translation, summarization, …)
Producing (generation, translation, etc):
What do I want to say? (Language generation)
How do I say a given word string? (Text-to-speech synthesis)
How do I convey the importance of different parts of this thought, or my emotion? (Expressive synthesis)
Can I imitate another speaker’s voice? (Voice conversion)
Learning (embedding, etc)
What are the sounds in this language? (Phonetic unit discovery)
What are the units of meaning (e.g. words) in this language? (Spoken term discovery)
What do the words in this language mean?
How are words combined in this language? (Grammar induction)
(Getting more into NLP…)
Connections¶
Representation learning & density estimation
Clustering \(\approx\) discrete representation learning
Is unsupervised learning all representation learning? Is it all density estimation? How about graph-based methods?
Advanced¶
The study of machine learning can be categorized as theories, models, and applications.
Model
How to model a problem?
Theory
Why does this model work?
Under what conditions will it have what performance?
Application
Fit the model or its variants to various type of data
Usually a model can be used for multiple problem. Take principal component analysis as an example,
Problems
dimension reduction
estimate latent variables
visualization
Model: principal component analysis
Theories
Identifiability: What is the weakest signal can we detect? Use random matrix theory.
Application:
Variants: probabilistic PCA, kernel PCA, …
Fitting: data for various domains …
We will focus on introducing models, but will also discuss the theories to analyze them.