Contents

K-nearest neighbors

\(K\)-nearest neighbors is a non-parametric method. It simply the application of nearest-neighbor smoothing on a graph.

It can be used for both classification and regression. The nearest-neighbor methods can also be applied to a graph with vertex attributes.

Classification from Data Matrix

If the input is a data matrix, \(K\)-nearest neighbors method look at the \(K\) points in the training set \(\mathcal{D}\) that are nearest to the test input \(\boldsymbol{x}_i\), denoted \(N_K \left( \boldsymbol{x}_i, \mathcal{D} \right)\). To define ‘nearest’, it requires a distance measure \(d(\boldsymbol{x}_i, \boldsymbol{x}_j)\), such as Euclidean distance.

To predict the class of observation \(\boldsymbol{x}\), use

\[\mathbb{P} (y=c\vert \boldsymbol{x}, \mathcal{D}, K) = \frac{1}{K} \sum_{j \in N_K (\boldsymbol{x}, \mathcal{D})} \mathbb{I}\left( y_j =c \right)\]

Validation data is used to decide the hyper-parameter \(K\).

Regression on Graph

If the input is a graph \(G=(V, E)\) with vertex attribute \(x _v\), then for new vertex \(i\) with unknown attribute but known edges, we can predict its attribute value by the average of those of its neighbors,

\[ \hat{\boldsymbol{x} }_i = \frac{\sum_{j \in \mathscr{N}_{i}} \boldsymbol{x} _{j}}{\left|\mathscr{N} _{i}\right|} \]

Note that there is no hyper-parameter \(K\).

Tuning

To choose optimal \(K\), we can use train-test split.

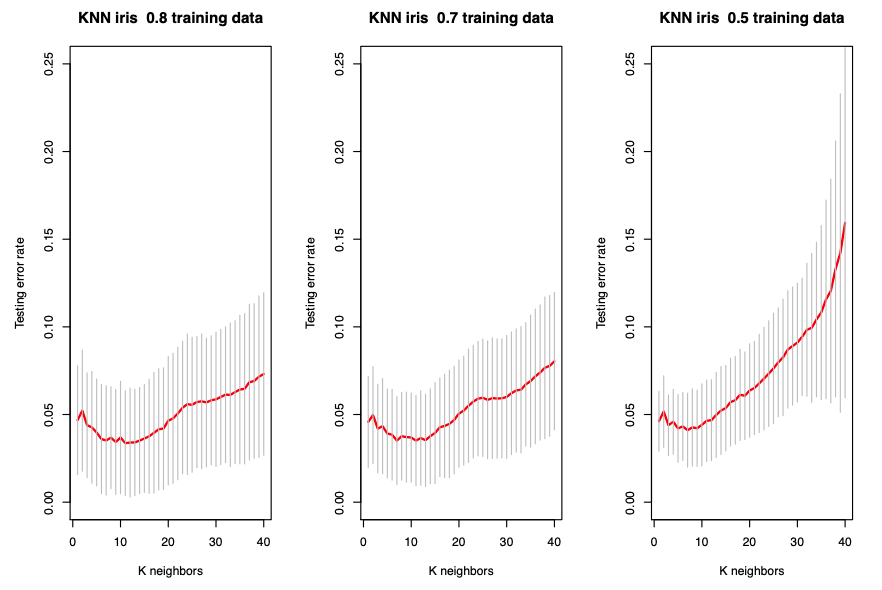
Fig. 80 Random train-test split for different ratios [Wang 2021]

As \(K\) increases from 1, the test error first decreases and then increases. The error bound increases.

Pros

  • Can express complex, non-linear, non-parametric boundaries

  • Very fast training

  • Simple, yet with good performance in practice

  • Reasonably good interpretability

Cons

  • It is an example of memory-based learning or instance-based learning. It stores all seen points.

  • Not among the best classifiers in terms of accuracy

  • Standardization is often necessary

  • Poor performance in high dimensional settings

  • In the graph case, how best to evaluate may not be clear in the case where \(\boldsymbol{x} _j\) is not observed for one or more \(j \in N_i\).

    • One solution to this dilemma is to redefine it in terms of only those vertices \(j \in V_i\) that are both adjacent to \(i\) and for which \(\boldsymbol{x} _j\) is observed.

    • Alternatively, we might impute values for the unobserved \(\boldsymbol{x} _j\), substituting, for instance, the overall average \(\frac{1}{\left\vert V_{obs} \right\vert}\sum _{k \in V_{obs}} \boldsymbol{x} _k\)

    • Although neither of these approaches is entirely satisfactory, imputation is likely to work better in practice, particularly when the relative number of missing observations is not small